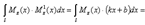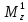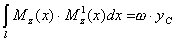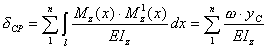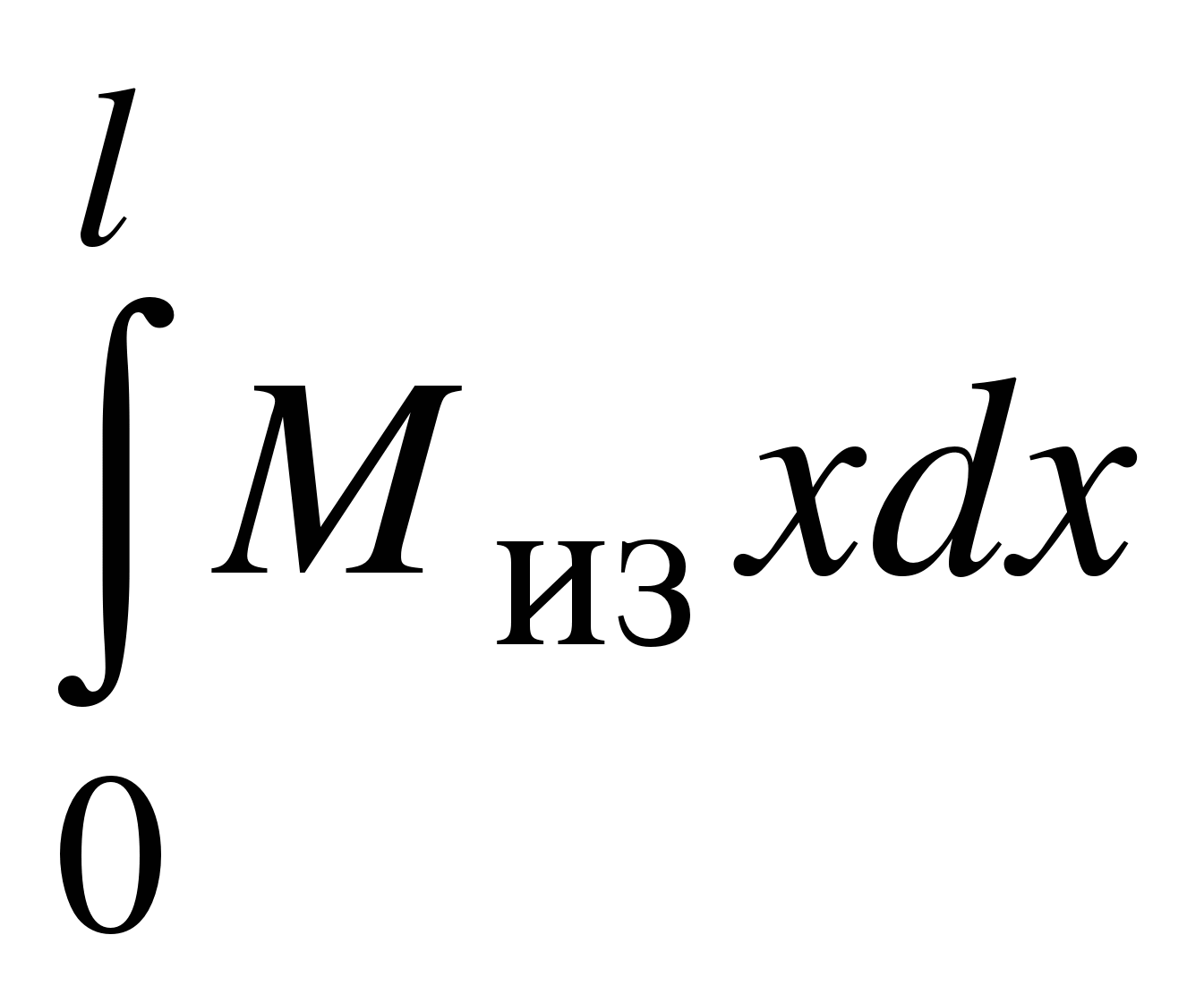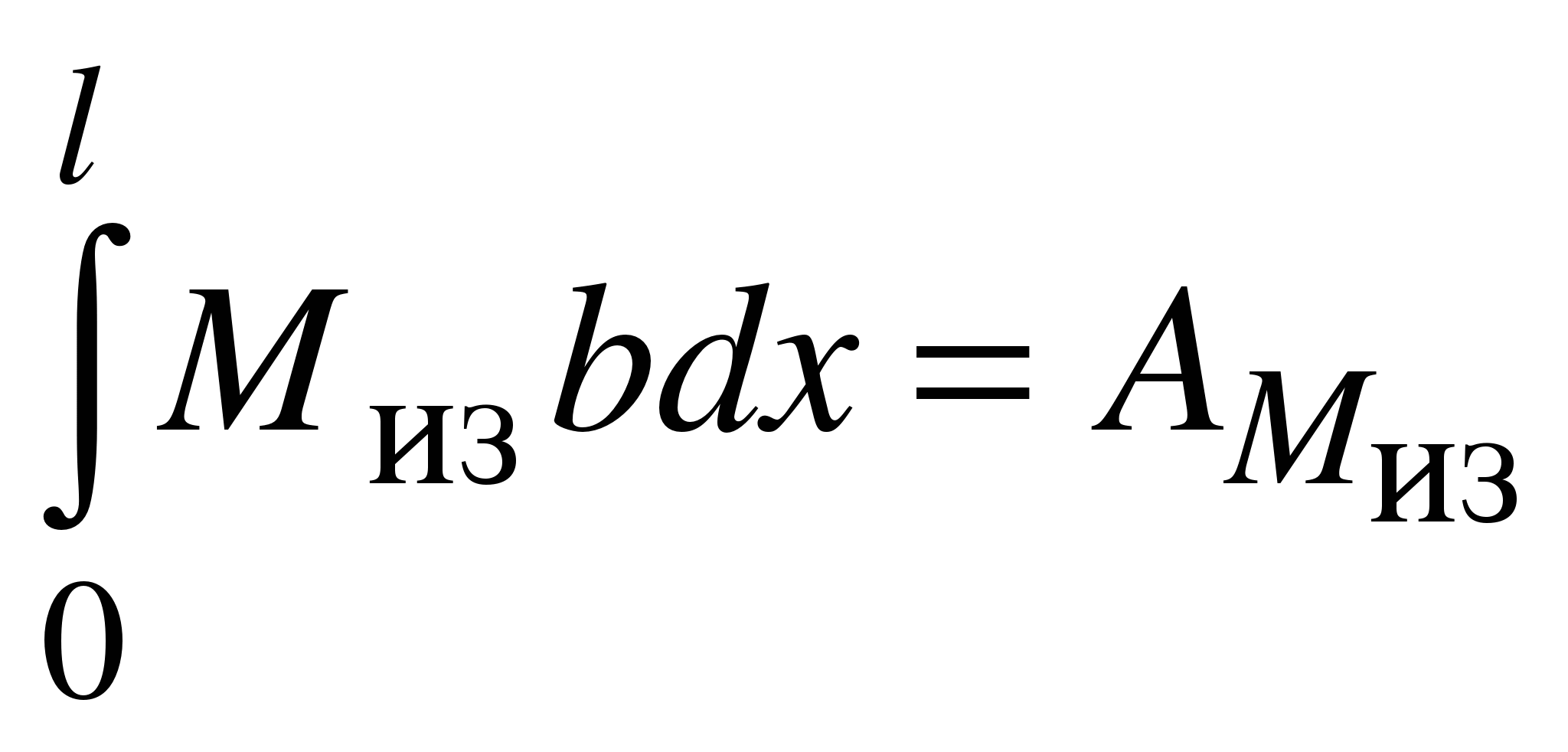Графоаналитический метод вычисления интеграла мора

7.7. Графоаналитический способ Верещагина

льно упрощающий вычисление интегралов в формуле Мора (7.18).

Интегралы Мора с точностью до постоянного множителя представляют собой интегралы от произведения двух функций вида:

где, по крайней мере, одна из функций (рис. 7.14)

является линейной ( постоянные величины).

Возьмём к примеру, интеграл

где — момент от единичной обобщённой силы – линейная функция, — в общем случае – криволинейная функция.

Подставляя выражение для в выражение для и производя почленное интегрирование, найдём:

Из рис. 7.14 следует, что есть элементарная площадь кри-

волинейной эпюры, — статический момент этой элементар-

ной площади относительно оси Поэтому:

Из полученной формулы (7.20) следует простое правило вычисления интегралов Мора: интеграл с точностью до постоянного множителя равен произведению площади криволинейной эпюры на ординату взятую из прямолинейной эпюры под центром тяжести криволинейной эпюры.

На первый взгляд, описанный графоаналитический способ вычисления интегралов Мора не даёт упрощений, т.к. всё равно приходится вычислять площадь криволинейных эпюр. Однако встречающиеся на практике эпюры могут быть разбиты на ряд простейших – прямоугольник, треуголь-ник, симметричную квадратичную параболу и др. Эти эпюры приведены на рис. 7.15.

В первом случае во втором в третьем в четвёртом

Рассмотрим несколько сложных эпюр (рис. 7.16): а) эпюра разбивае-

тся на симметричную параболу, треугольник и прямоугольник; б) эпюра пересекает ось стержня, её можно дополнить сверху и снизу равными пло-

щадями и разложить на два треугольника, доказательство добавляемых площадей элементарно: из подобия заштрихованных треугольников следует откуда что и доказывает утверждение;

в)эпюра разбивается на симметричную параболу и два треугольника, соответствующих случаю (б).

Источник

Графоаналитический способ вычисления перемещений(метод Верещагина)

В 1925 г. А. Н. Верещагин предложил простой графоаналитический прием вычисления интеграла Мора в случаях, когда эпюра (или Mz) ограничена прямыми линиями. По существу это прием графоаналитического вычисления определенного интеграла от произведения двух функций f(x) и φ(x), из которых одна, например φ(x), линейная, т. е. имеет вид

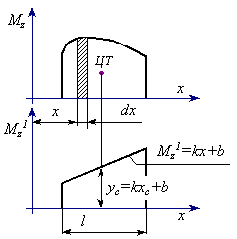
Рассмотрим участок балки, в пределах которого эпюра изгибающих моментов от единичной нагрузки ограничена одной прямой линией =kx+b, а изгибающий момент от заданной нагрузки изменяется по некоторому произвольному закону Mz. Тогда в пределах этого участка

Второй интеграл представляет собой площадь ω эпюры Mz на рассматриваемом участке, а первый — статический момент этой площади относительно оси y и поэтому равен произведению площади ω на координату ее центра тяжести xc. Таким образом

,

Здесь kx_c+b — ордината y_c эпюры под центром тяжести площади ω. Следовательно,

Произведение ωy_c будет положительным, когда ω и y_c расположены по одну сторону от оси эпюры, и отрицательным, если они находятся по разные стороны от этой оси.

Итак, по способу Верещагина операция интегрирования заменяется перемножением площади ω одной эпюры на ординату y_c второй (обязательно линейной) эпюры, взятой под центром тяжести площади ω.

Важно всегда помнить, что такое «перемножением» эпюр возможно лишь на участке, ограниченном одной прямой той эпюры, с которой берется ордината y_c. Поэтому при вычислении перемещений сечений балок способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда

24) Расчет статически неопределимых систем методом сил

Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.

Метод сил. При расчете по методу сил основными искомыми величинами являются усилия в лишних связях. Знание усилий в лишних связях позволит по методу сечений выполнять полный расчет по определению усилий, возникающих в поперечных сечениях элементов заданной системы.

Для продолжения скачивания необходимо пройти капчу:

Источник

Сапромат / ГРАФОАНАЛИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ И УГЛОВ ПОВОРОТА БАЛКИ ПРИ ИЗГИБЕ

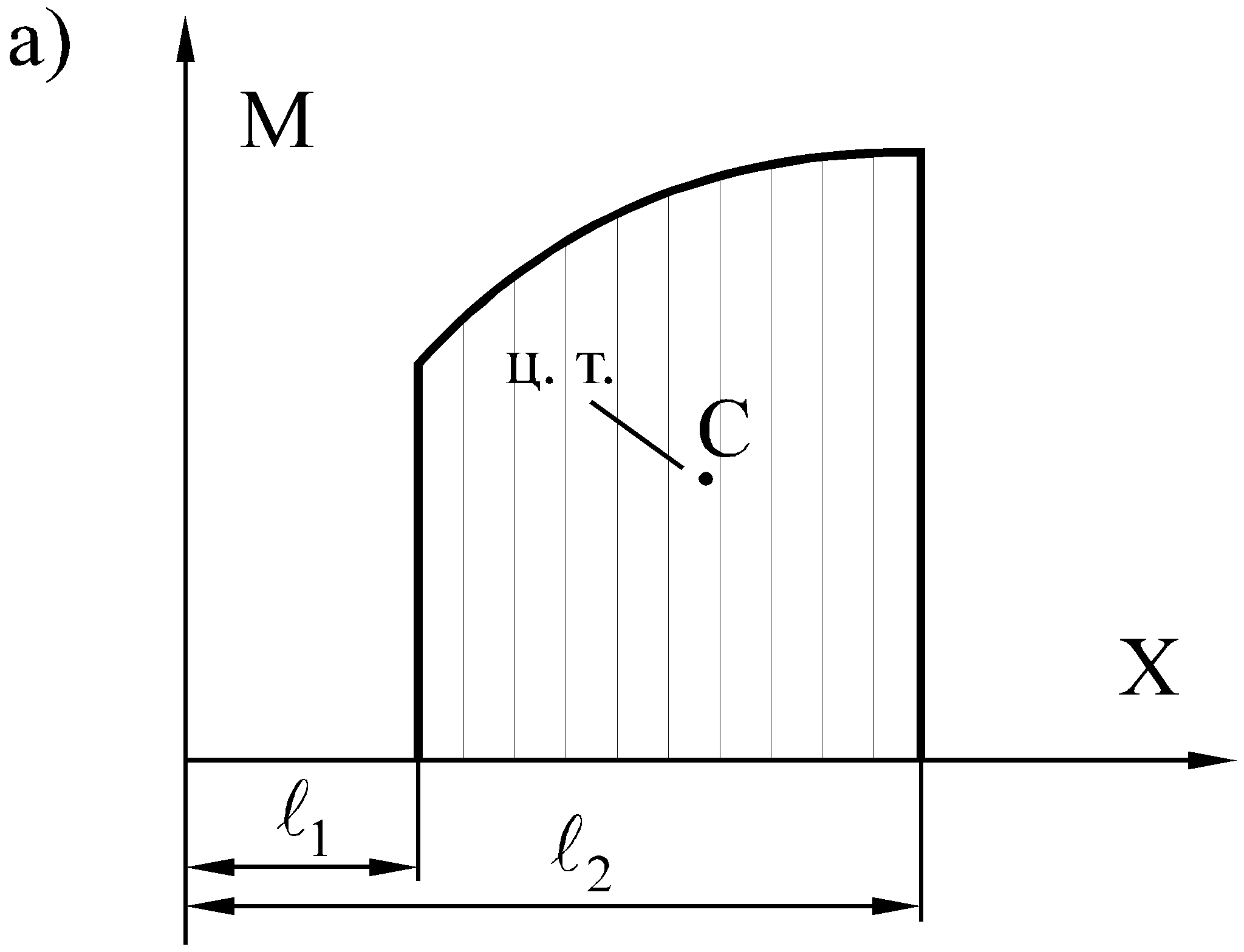
Способ Верещагина Помимо непосредственного вычисления интеграла Мора можно пользоваться графоаналитическим приемом: способом перемножения эпюр или правилом Верещагина. Для вывода формулы, предложенной Верещагиным, возьмем один участок балки. Построим эпюру М_из от внешних сил. В сечении, где нужно найти прогиб балки, прикладываем единичную силу и строим от нее эпюру изгибающих моментов М₁. Часть этой эпюры на той же длине балки приведена на рис. В общем случае М_из описывается уравнением f(x), а эпюра от единичной нагрузки – уравнением прямой М₁ = ах + b. Подставляем эти значения в интеграл Мора: Выражение представляет собой статический момент площади.

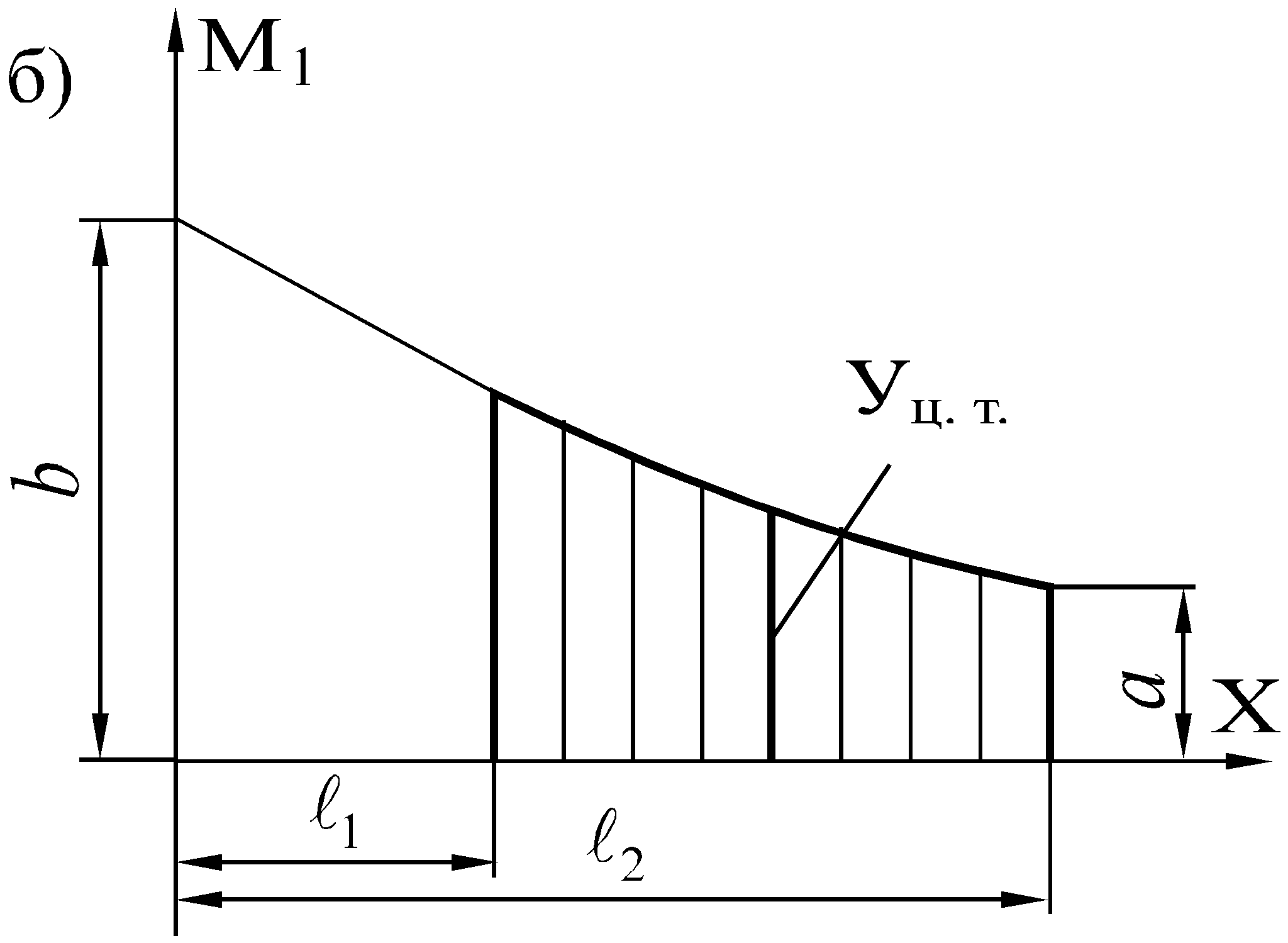
Второй интеграл имеет смысл площади эпюры изгибающих моментов внешних сил.

Поскольку , то окончательно получим , где – ордината эпюры моментов М₁ от единичной силы под центром тяжести эпюры М_из. Для определения перемещений с учетом нескольких грузовых участков надо полученную формулу применить для всех этих участков Таким образом, чтобы использовать правило Верещагина, необходимо: 1. Построить эпюры изгибающих моментов от внешних сил. 2. В том сечении, где надо определить прогиб, приложить единичную силу (для нахождения угла поворота сечения приложить единичный момент). 3. Построить эпюры изгибающих моментов от единичной силы (от единичного момента). 4. Вычислить площадь А_{М из} эпюры на каждом участке балки. 5. Умножить эту площадь на ординату единичной эпюры, находящуюся под центром тяжести эпюры моментов внешних сил. 6. Вычислить y_C либо  по формуле (14.7). При этом необходимо учитывать тот факт, что перемножение эпюр с одинаковыми знаками дает “плюс”, с разными “минус”. Положительные y_C и  всегда направлены в сторону действия соответствующей им единичной силы или единичного момента. Для упрощения процесса расчета деформаций сечений балки целесообразно воспользоваться готовой таблицей, где приведены формулы, по которым можно найти произведение А_{М из} y_ц.т. в зависимости от вида эпюр М_из и М₁ (см. таблицу).

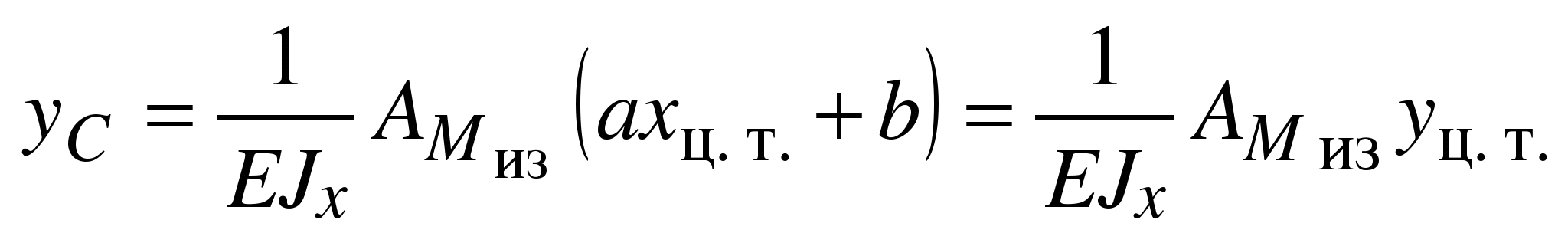
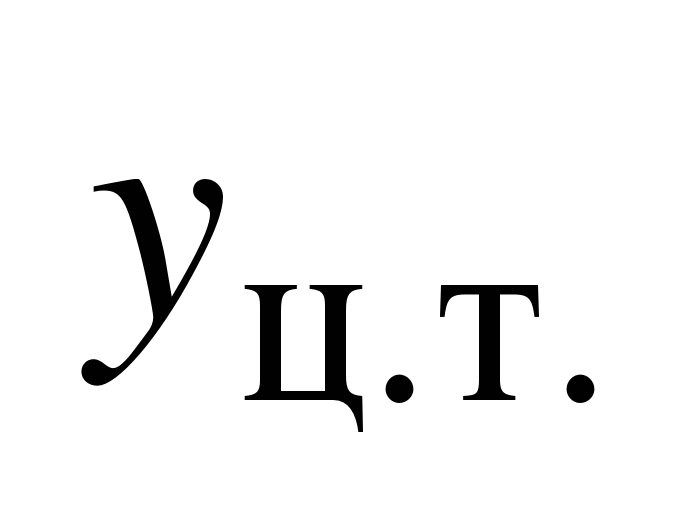
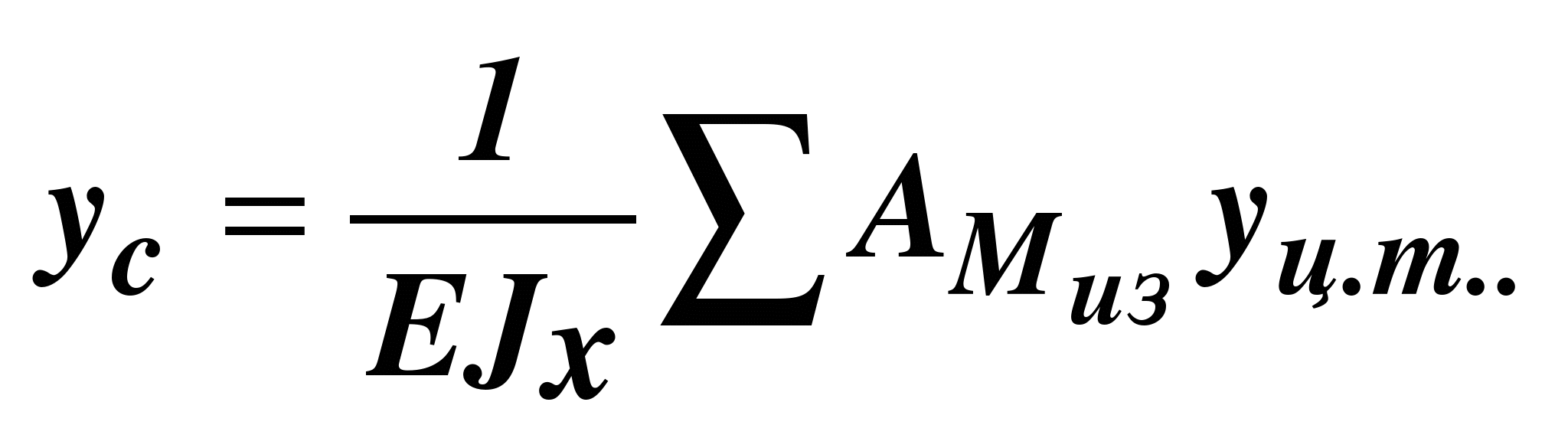
Таблица – Значения, используемые при применении правила Верещагина

Эпюры M, построенные от внешних нагрузок

Эпюры М₁, построенные от единичных сил и моментов

Источник

11.5 Графо – аналитический метод взятия интегралов (способ Верещагина)

Основным недостатком определения перемещений при помощи интеграла Мора является необходимость составления аналитического выражения подынтегральных функций. Это особенно неудобно при определении перемещений в стержне, имеющем большое количество участков. Однако, если он состоит из прямых участков с постоянной в пределах каждого участка жесткостью, операцию интегрирования можно упростить. Это упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках оказываются линейными.

Этот способ применим только для прямолинейных участков, т.к. в этом случае единичная эпюра всегда носит единичный характер.

Пусть имеется эпюра внешних сил М_р (грузовая эпюра), обозначим ее площадь Ω_р (рис.11.22).

Рис. 11.22 Эпюра внешних сил

Для определения перемещения необходимо вместо вычислений интеграла Мора умножить площадь грузовой эпюры Мр на ординату, взятую на единичной эпюре под центром тяжести грузовой (нелинейной) эпюры.

где р – площадь грузовой эпюры,

— ордината единичной эпюры под центром тяжести грузовой эпюры.

11.6 Универсальная формула трапеции

Рис. 11.24 Эпюра внешних сил

где — если есть распределенная нагрузка и ,

В формуле трапеции все ординаты берутся с учетом знака.

Рис. 11.25 Эпюры Мр и М₁

Замечание: если в результате вычислений перемещение получилось со знаком «−», то направление перемещения противоположно направлению единичного усилия.

Заключение

Сопротивление материалов является одной из основных общеобразовательных инженерных дисциплин и играет существенную роль в формировании инженера почти любой специальности. Особенно большое значение сопротивление материалов имеет для механических, машиностроительных и строительных инженерных специальностей.

В связи с повышением энерговооруженности и быстроходности, уменьшением удельной материалоемкости машин, насыщением их гидро- и пневмомеханизмами возникла насущная необходимость повышения качества расчетных методов прикладной механики при разработке конструкций машин.

Настоящее пособие содержит ясную физическую трактовку явлений и логические выводы, задачи в четкой постановке; изложение опирается на строгий, но, по возможности, простой математический аппарат и строится на основе сведений, полученных при изучении естественнонаучных дисциплин.

Пособие будет полезно не только инженерам – конструкторам и производственникам всех специальностей, встречающимися в практической деятельности с расчетами на прочность, но будет с успехом использовано студентами, аспирантами, преподавателями и научными работниками.

Источник