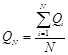Анализ условий формирования и расчет основных статистических характеристик стока реки Кегеты
Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .
Гипсографическая кривая дает наглядное представление о распределении площади бассейна по высотным зонам. Для ее построения весь диапазон высот в бассейне разбивается на 8 высотных ступеней и измеряются площади, расположенные между горизонталями с отметками этих ступеней и линией водораздела. Чем больше амплитуда высоты в бассейне, тем большие интервалы высоты берутся для отдельных ступеней.
>Наивысшей точкой бассейна Кегеты является точка с отметкой 4444 м, минимального значения высота достигает в районе створа – 1500 м, амплитуда составляет 2944 м. В соответствие с методикой, этот интервал следует разбить на 8 высотных ступеней. Полученные таким образом значения горизонталей послужили основой разбиения площади бассейна, представленного на рис. 7. Высотные отметки горизонталей и результаты вычисления площадей, заключенных между ними, приведены в табл. 3.
По данным измерений площадей и отметкам горизонталей строится график распределения площадей по высотным зонам, показывающий размеры площадей, лежащих между высотными отметками. Он имеет вид столбчатой диаграммы, по горизонтали откладываются площади, по вертикали – высотные отметки. Для Кегеты этот график представлен на рис. 8.
После того как график распределения площадей построен, строится кривая нарастания площадей по высотным зонам – гипсографическая кривая, которая может быть получена путем последовательного суммирования площадей, отложенных по оси абсцисс на предыдущем графике. Точки гипсографической кривой откладываются на нижних границах высотных интервалов и соединяются плавной линией. На графике под масштабом площадей наносится шкала процентов из расчета, что общая площадь бассейна равна 100%. Точке на кривой с абсциссой 50% и будет соответствовать высота на оси ординат, которую можно считать средней высотой водосбора. Гипсографическая кривая бассейна р. Кегеты построена на рис. 9
Таблица 3. Ведомость измерения площадей высотных зон бассейна р. Кегеты
Высотные отметки горизонталей, м
Площадь высотной зоны, км2
К геоморфологическим коэффициентам относятся коэффициент озерности, коэффициент заболоченности и коэффициент залесенности. Они рассчитываются соответственно как процентное отношение суммарной площади озер, болот и лесов, расположенных в бассейне некоторой реки, к площади водосбора этой реки. Например, коэффициент озерности определяется по формуле (9):
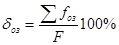
Насколько можно установит по карте на рис. 1, бассейн р. Кегеты содержит озеро. Леса не отображены на карте.
2.2 Климатические факторы стока
Распределение осадков по поверхности суши зависит от удаления местности от океана, рельефа местности и растительного покрова. По мере удаления от океана количество постепенно уменьшается. В горных районах склоны, обращенные к влагоносным ветрам, получают больше осадков, чем противоположные. Влияние рельефа сказывается в том, что с повышением местности количество выпадающих осадков обычно увеличивается. Увеличение количества осадков с высотой обычно происходит до отметок 3000 – 3500 м над уровнем моря, а выше эта зависимость уменьшается или прекращается.
Опираясь на карты источника, можно отметить большую увлажненность бассейна Кегеты осадками ввиду благоприятных условий географического расположения. Среднегодовые суммы осадков здесь на большей части территории на высотах от 1300–1400 м до 2300–2500 м превышают 1000 мм. Выше и ниже этих пределов осадков выпадает меньше, и при подъеме по юго-западному склону Кыргызского хр. до высот 3500 – 3800 м их количество уменьшается до 600 мм.
Процесс испарения состоит в том, что вода из жидкого или твердого состояния переходит в газообразное. К факторам, увеличивающим испарение, относятся повышение температуры и увеличение скорости ветра, усиливающее турбулентное перемешиванию масс воздуха, соприкасающихся с испаряющей поверхностью. Кроме того, на интенсивность испарения влияет влажность почвы, солнечная радиация, которые обуславливают жизнь растений и их рост, парциальное давление (упругость) водяного пара в воздухе и др.
Температура в долине р. Кегеты в среднем уменьшаются с высотой от +20 до +10 °С в июле и от -4 до -14 °С в январе. Средняя влажность в июле составляет 40 – 55%, а в январе – 55 – 60%. Среднегодовая испаряемость в бассейне Кегеты равномерно уменьшается от низовий к верховьям от 1200–1300 мм до 600 мм. В целом, бассейн Кегеты по классификации В. Кеппена и А.В. Вознесенского относится к бореальному типу климата с ясно выраженной зимой и летом и достаточным увлажнением, и лишь высокогорные участки Кыргызского хребта имеют холодный тундровый тип климата.
3. Сток и его распределение
3.1 Определение нормы годового стока и его статистических характеристик
Нормой годового стока Q0 называется среднее его значение за многолетний период такой продолжительности, при увеличении которой полученное среднее существенно не меняется, включающий несколько полных четных циклов колебаний водности реки при неизменных географических условиях и одинаковом уровне хозяйственной деятельности в бассейне реки. Норма годового стока, или средний многолетний сток, является основной и устойчивой характеристикой, определяющей общую водность рек и потенциальные водные ресурсы данного бассейна или района.
Согласно «Указаниям по определению расчетных гидрологических характеристик» (СН 435–72) /7,8,13/, продолжительность периода наблюдений считается достаточной для установления расчетных значений нормы годового стока, если рассматриваемый период репрезентативен и относительная средняя квадратическая ошибка многолетней величины eQ0 не превышает 5…10%, а коэффициент вариации (изменчивости) eсv – 10…15%.
Норма годового стока, как всякая средняя арифметическая величина статистического ряда, может быть определена по формуле:

где QN — норма годового стока, Qi – годовые значения стока за длительный период (N лет).
Среднегодовой расход воды р. Кегаты за 1927–1975
Источник
Гипсографическая кривая
Общую картину соотношения различных высот и глубин на Земле можно получить статистическим способом, путём измерения на картах площадей, занятых наиболее характерными ступенями высот и глубин.
Для этой цели необходимы карты земного шара, на которых рельеф суши изображён изогипсами, или горизонталями (линиями, соединяющими точки одинаковой высоты), проведёнными через определённые интервалы высот, а глубины океана показаны изобатами (линиями, соединяющими точки одинаковой глубины), проведёнными через определённые интервалы глубин. Такого рода вычисления делались неоднократно.
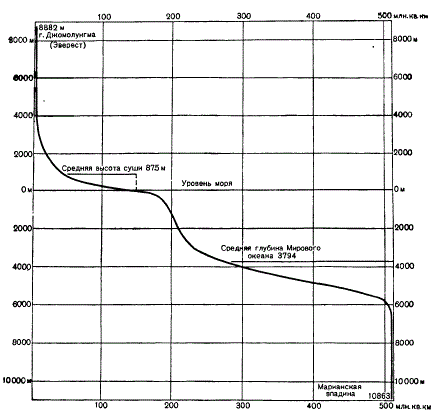
Данные, содержащиеся в таблице, изображают для наглядности в виде так называемой гипсографической кривой. По оси ординат откладывают глубины и высоты, а по оси абсцисс — площади, занятые соответствующими ступенями высот и глубин, в миллионах квадратных километров или в процентах от площади земной поверхности, в соответствии с чем вся ось абсцисс принимается либо за 510 млн. кв. км, либо за 100%.
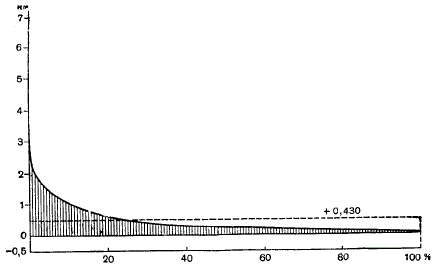
Гипсографическая кривая СССР. Высшая точка — пик Сталина (7495 м), низшая — депрессия Карагие на Мангышлаке (—132 м). Площадь СССР (22 369 290 кв. км) принята на оси абсцисс за 100%.
Построение графика производится следующим образом. Сначала на оси абсцисс откладывается отрезок, отвечающий площади, которую занимает наибольшая ступень высот (3000—8882 м; последняя цифра — высота Эвереста); из конца этого отрезка восстанавливают ординату до высоты нижнего предела данной ступени высот (т. е. до 3 тыс. м). Затем на оси абсцисс (от точки, где кончился первый отрезок) откладывают второй отрезок, отвечающий площади, занимаемой следующей ступенью высот (3—2 тыс. м), и из его конца восстанавливают ординату до высоты нижнего предела этой второй ступени и т. д. Затем все концы ординат соединяют с помощью лекала плавной кривой; окончание её должно отвечать наибольшей глубине Марианской впадины. Это и будет гипсографическая кривая, т. е. диаграмма, отражающая соотношение площадей, занятых различными ступенями высот и глубин на земном шаре.
Гипсографические кривые можно строить не только для всего земного шара, но и для любого материка, острова, океана или моря в отдельности; в этих случаях шкала высот и глубин (её общая амплитуда и размеры ступеней) будет несколько другая (конкретный материал подскажет, какую форму ей удобно придать), а произвольно выбранная длина оси абсцисс будет отвечать площади того объекта (участка суши или водоёма), для которого диаграмма делается. Средняя высота территории СССР над уровнем океана оказалась равной 430 м.
По точно построенной гипсографической кривой всегда можно получить необходимые цифровые данные. Желая, например, узнать, какова площадь глубин, заключённых между изобатами 2000 и 6000 м, проводим от точек —2000 и —6000 горизонтальные линии до пересечения с гипсографической кривой, а затем из точек пересечения опускаем перпендикуляры на ось абсцисс; отрезок оси абсцисс, заключённый между обоими перпендикулярами, как раз и будет представлять искомую площадь, выраженную в принятом для диаграммы масштабе.
Достоинство гипсографической кривой — не только в её наглядности, но и в том, что своими очертаниями она фактически даёт обобщённый идеальный профиль поверхности твёрдой земной коры. Мы видим, что материки и океанические впадины — это основной рельеф земного шара, и что материки выглядят как плоскогорья, поднимающиеся над океаническим дном. Так как средняя высота суши 875 м, а средняя глубина Мирового океана около 3800 м, то средняя высота материков-плоскогорий над дном моря составляет 4675 м. На суше преобладают высоты менее 1 тыс. м, занимающие по площади 3/4 поверхности суши; стало быть, горы являются второстепенной деталью в рельефе материков. На графике также хорошо видно, что материковая отмель и материковый склон (т. е. область глубин от 0 до 2500 м) действительно принадлежат ещё материку, образуя те склоны, которыми материк-плоскогорье опускается к своему подножию — ложу океана. В океане преобладают глубины от 3 до 6 тыс. м; они занимают 75% его площади; следовательно, глубоководные океанические впадины такая же второстепенная деталь в рельефе морского дна, как и горы в рельефе континентов.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник
Построение и анализ гипсографической и батиграфической кривой
Гипсографическая и батиграфическая кривая – линии, показывающие соотношение площадей, занимаемых на Земле различными высотами к глубинами. Для ее построения используются данные табл.1.
Таблица 3Соотношение площадей земной поверхности,
расположенных на различных высотах и глубинах
| Суша | Океан | ||
| Высота, м | Площадь ступеней высот, млн. км 2 | Глубина, м | Площадь ступеней глубин, млн. км 2 |
| 8848 — 3000 | 8,4 | 0 — 200 | 27,1 |
| 3000 — 2000 | 11,2 | 200 — 1000 | 16,0 |
| 2000 — 1000 | 22,5 | 1000 — 2000 | 15,8 |
| 1000 — 500 | 28,7 | 2000 — 3000 | 30,8 |
| 500 — 200 | 39,7 | 3000 — 4000 | 75,8 |
| 200 — 0 | 37,6* | 4000 — 5000 | 114,7 |
| 5000 — 6000 | 76,8 | ||
| 6000 — 11022 | 5,0 |
* Включая площадь суши, находящуюся ниже уровня Океана — 0,8 млн. км 2
Гипсографическая и батиграфичекая кривая (рис. 1) строится на миллиметровой бумаге. На оси абсцисс откладываются площади ступеней высот и .глубин, на оси ординат – высоты и глубины. Рекомендуемый масштаб: горизонтальный – в 1 см 20 млн. км 2 , вертикальный – в 1 см 1000 м. Порядок построения кривой следующий: из начальной точки (х) восстанавливается перпендикуляр до наибольшей высоты (8848 м)-х1, на оси абсцисс от начала графика в масштабе откладывается
Рис. 1. Гипсографическая и батиграфическая кривая Земли
площадь первой ступени высот (8858-3000 м – 8,4 млн. км 2 ), точка f и восстанавливается перпендикуляр ( Ш ) до точки U – до нижнего предела данной ступени высот (3000 м).
Далее от точки f по оси абсцисс откладывается площадь второй ступени высот (11,2 млн км 2 ) – f d , а затем из точки ( d) восстанавливается перпендикуляр до нижнего предела высоты данной ступени (2000 м) – dz . От точки d откладывается площадь третьей ступени высот и т.д. Так же последовательно за высотой суши откладываются и площади средних глубин океанов. Только сами глубины откладываются вниз от оси абсцисс. Соединив плавной линией вершины всех перпендикуляров, получим гипсографическую и батиграфическую кривую. Кривая разделит нулевую линию на два отрезка, соответствующие по длине в масштабе площади, занимаемой сушей (149 млн. км 2 ) и Океаном (361 млн. км 2 ).
Часть кривой, находящейся выше нулевой линии (уровня Океана), носит название гипсографической кривой (от греч. hipsos – высота, grapho – пишу) и показывает соотношение площадей, расположенных на различных высотах. Часть кривой ниже уровня Океана, показывает соотношение площадей, расположенных на различных глубинах, и носит название батиграфической кривой (от греч. batos – глубина, grapho –пишу).
Определить и показать линиями на чертеже:
1. Средний уровень земной коры (твердой земной поверхности).
2. Средний уровень земной поверхности (физической поверхности Земли).
3. Среднюю высоту суши.
4. Среднюю глубину океана.
1. Средний уровень земной коры – уровень, на котором располагалась бы выровненная поверхность Земли без воды. Для определения среднего уровня земной коры необходимо изобразить площадь (S) фигуры, ограниченной гипсографической и батиграфической кривой и прямыми уу1 , и у1к, т.е. luzcky1 , в виде прямоугольника, основание которого представлено прямой y1k .
Из конечной точки гипсографической и батиграфической кривой (k) восстанавливаем перпендикуляр на ось абсцисс (km) и ось ординат (ky1). Подсчитываем площадь фигуры luzcky1 (вначале подсчитываем целые квадраты, а затем их части). Так как по оси абсцисс нанесена площадь, занимаемая различными ступенями высот и глубин, а по оси ординат – высоты, то площадь фигуры будет соответствовать объему земной коры выше уровня 11022 м. Определяем (в см) длину основания прямоугольника y1k. Высота прямоугольника определяется:
Высота откладываемой точки у, вверх по оси ординат. Из вершины этой высоты проводится линия, параллельная оси абсцисс. Эта линия и будет соответствовать среднему уровню земной коры, т.е. уровню, на котором находилась бы поверхность земной коры, если весь объем земной коры, находящийся выше уровня 11022 м, расположить ровным слоем, т.е. линия должна пройти ниже уровня океана. Числовое значение уровня земной коры (в м) определяется по масштабу оси ординат и наносится на линии среднего уровня земной коры.
2. Средний уровень земной поверхности (физической поверхности земли) – уровень, на котором расположится поверхность водной оболочки, если она ровным слоем покрывает Землю выше уровня земной коры (твердой земной поверхности). Подсчитываем площадь фигуры cmk. Эту площадь представляем в виде прямоугольника над уровнем земной коры, т.е. площадь фигуры cmk (в см 2 ) делим на хm (в см) и полученную высоту откладываем по оси ординат вверх от линии среднего уровня земной коры. Пользуясь масштабом, находим цифровое значение среднего уровня земной поверхности. Параллельно оси абсцисс проводим линию среднего уровня земной поверхности и подсчитываем; значение в метрах.
3. Средняя высота суши определяется делением площади фигуры xlc на длину прямой хс, т.е. делением объема земной коры выше современного уровня Океана на площадь, занимаемую сушей. Полученную высоту откладываем на оси ординат выше точки 0. Проводим линию средней высоты суши и надписываем значение в метрах.
4. Среднюю глубину океана определяем делением площади фигуры cmk на длину линии cm . Полученную величину откладываем от точки 0 вниз на оси ординат. Наносим линию средней глубины Океана параллельно оси абсцисс и надписываем ее значение в метрах.
Дать анализ кривой. Указать: а) какие площади занимают горы, плоскогорья, низменности, материковая отмель, материковый склон, ложе океана, глубоководные океанические впадины; б) какие ступени высот и глубин на Земле наиболее характерны.
Познакомиться с понятиями «Геотектура», «Морфоструктура» и «Морфоскульптура», дать их определение, объяснить принципы, положенные в их основу. Привести на карте мира примеры различных категорий гео-, морфоструктур и морфоскульптур. На контурной карте мира на каждом материке постройте круговую диаграмму (табл.4), показывающую соотношение площадей (%), занятых основными типами геотектуры и морфоструктуры: равнинно-платформенными я орогеническими. Последние подразделите (используя штриховку) в соответствии с возрастом складчатости. Сравните диаграммы, построенные для разных материков с данными для суши в целом. Какие наблюдаются закономерности в соответствии основных типов геотектуры и морфоструктуры для суши в целом и для отдельных материков? Чем они объясняются? Какие отклонения от общих закономерностей наблюдаются и с чем они связаны?
Таблица 4.Площади суши, занимаемые основными типами геотектуры и
морфоструктуры (по Н.П. Неклюковой, 1977)
| Типы геотектуры морфоструктуры | Суша (без обл. занят, современ. ледников, щитами) | Европа | Азия | Африка | Северная Америка | Южная Америка | Австралия |
| I. Равнинно-платформен-ные области: | 64,0 | 70,3 | 43,0 | 84,1 | 61,0 | 76,6 | 73,8 |
| 1. Цокольные равнины и плоскогорья древних платформ | 16,6 | 11,9 | 3,0 | 25,8 | 23,0 | 18,6 | 37,0 |
| 2. Равнины и плато древних плит | 31,0 | 34,5 | 13,8 | 48,4 | 28,8 | 47,8 | 24,3 |
| 3. Равнины и мелкосопочник молодых платформ | 5,6 | 12,9 | 12,9 | – | – | 3,0 | – |
| 4. Кряжи и плоскогорья молодых платформ | 0,3 | 1,9 | 0,3 | – | – | – | – |
Продолжение таблицы 4
| 5. Краевые низменности | 8,6 | 8,0 | 9,7 | 9,0 | 9,2 | 3,3 | 11,8 |
| 6 . Вулканические плато | 1,9 | 1,1 | 3,3 | 0,9 | 3,9 | 0,7 | |
| II Горные (орогенические) области: | 36,0 | 29,7 | 57,0 | 15,9 | 39,0 | 23,4 | 26,2 |
| 1.Горы и нагорья областей докембрийской складчатости | 3,3 | _ | 2,8 | 7,2 | 1,7 | 3,4 | _ |
| 2. Палеозойской складчатости | 6,2 | 12,8 | 8,6 | 0,6 | 4,3 | 3,3 | 10,1 |
| 3. Мезозойской складчатости | 6,6 | _ | 6,0 | _ | 23,5 | 0,6 | _ |
| 4. Кайнозойской складчатости | 11,2 | 15,8 | 15,3 | 2,1 | 4,3 | 14,7 | 10,1 |
| 5. Вулканические горы и нагорья | 1,2 | 0,2 | 4,2 | 3,3 | 5,2 | 1,4 | 2,0 |
| 6. Внутриплатформенные горы | 4,4 | 0,9 | 10,6 | 2,7 | – | – | 4,0 |
| 7. Межгорные равнины | 3,1 | – | 9,5 | – | – | – | – |
1. Что такое а) платформа? б) складчатое сооружение? в) геосинклиналь? Каково строение материковой и океанической платформ?
2. Сопоставить тектоническую и физическую карты мира (ФГАМ, Географический атлас для учителя средней школы) и выявить, какой тип рельефа суши – равнинный или горный (назовите конкретные горы и равнины) преобладает в областях распространения: а) древних платформ, б) каледонской, в) герцинской, г) мезозойской и д) альпийской складчатости.
3. К каким тектоническим областям приурочены величайшие на Земле равнины и высочайшие горы?
4. Нанесите на контурную карту высочайшие горные вершины кружочками и отметками абсолютных высот (табл. 5).
| Вершина | Высота, м | Горная система |
| Джомолунгма | Гималаи | |
| Канченджанга | Гималаи | |
| Джаулагири | Гималаи | |
| Нангапрабат | Гималаи | |
| Чогори | Каракорум | |
| Улугмустаг | Куньлунь | |
| Пик Коммунизма | Памир | |
| Килиманджаро | ||
| Пик Ленина | Памир | |
| Пик Победы | Тянь-Шань | |
| Хан-Тенгри | Тянь-Шань | |
| Монблан | Альпы | |
| Мак-Кинли | Кордильеры | |
| Аконкагуа | Анды | |
| Косцюшко | Австрийские Альпы |
1. Дать анализ карты распределения радиационного баланса на Земле (рис. 2):
А. Каковы общие закономерности в изменении радиационного баланса на поверхности Земли?
Б. Почему максимальные величины радиационного баланса приходятся на поверхность океана?
В. Какие районы на земном шаре и почему имеют наибольшие величины радиационного баланса?
2.Дать анализ составляющих теплового баланса континентов и океанов (табл.6).
Таблица 6. Тепловой баланс континентов и океанов, кДж/(см 2 • год)
| Составляющие теплового баланса | Континенты или части света | Океаны | ||||||
| Европа | Азия | Африка | Северная Америка | Южная Америка | Австралия | Атлантический | Тихий | Индийский |
| Радиационный баланс R | ||||||||
| Затраты тепла на испарение LE | ||||||||
| Турбулентный поток тепла от подстилающей поверхности к атмосфере Р |
А. Выявить общие закономерности в соотношении между компонентами теплового баланса для континентов и океанов.
Б. Сравнить приходную и расходную части теплового баланса континентов и океанов и объяснить существующие между ними различия.
В. Объяснить различия в величинах расходной части теплового баланса разных континентов.
3.Вычислить тепловой баланс ландшафтно-климатических зон (табл. 7)и на основании полученных данных выявить соотношение между приходными и расходными частями теплового баланса различных зон.
Рис. 2. Распределение радиационного баланса на Земле
Таблица 7. Компоненты теплового баланса различных
ландшафтно-климатических зон, кДж/(см 2 • год)
| Зоны | Прямая радиация | Рассеянная радиация | Отраженная радиация | Эффективное излучение | Затраты тепла на испарение LE | Тепловой баланс |
| Арктическая | – | |||||
| Тундра | ||||||
| Тайга | ||||||
| Смешанные леса | ||||||
| Лесостепь | ||||||
| Степь | ||||||
| Полупустыня | ||||||
| Пустыни |
Дать анализ карты годовой амплитуды температуры воздуха (рис. 3).
А Каковы закономерности изменения годовой амплитуды температуры воздуха в направлении от экватора к полюсам? Какова амплитуда температуры воздуха в приэкваториальных, тропических, умеренных и приполярных широтах? На каких широтах земного шара наблюдаются максимальные амплитуды температуры воздуха?
Б. Выявить районы с максимальными и минимальными годовыми амплитудами температуры воздуха.
В. Сравнить годовые амплитуды температуры воздуха суши и океана одних и тех же широт.
Г. Сравнить годовые амплитуды температуры воздуха Северного и Южного полушарий. Объяснить выявленные закономерности.
Рис. 3. Средняя годовая амплитуда температуры воздуха
А. Вычертить график зависимости распределения годовых температур и амплитуд температур воздуха по параллелям от распределения суши и моря на поверхности Земли, по данным табл. 8.Дать анализ графика: а) указать, насколько постепенно изменяются среднегодовые температуры и годовые амплитуды воздуха от экватора к полюсам и как это связано с распределением суши и моря по параллелям; б) сравнить среднегодовые температуры и годовые амплитуды воздуха на одних и тех же широтах Северного и Южного полушарий. Дать объяснение выявленным закономерностям.
Примечание. Все данные табл. 8 наносят на один график. На оси абсцисс откладывают градусы широты (направо от нуля градусы широт Северного полушария, налево от нуля — Южного). Процент суши, годовые амплитуды и средние годовые температуры воздуха откладывают на оси ординат (положительные среднегодовые температуры – вверх от нуля графика, отрицательные – вниз). Процент суши для разных широт приводят в виде столбиковых диаграмм, распределение средних температур и амплитуд воздуха — в виде кривых.
Кривые проводят цветными карандашами.
Масштаб графика: для градусов широт – в 1 см 10°: для температур воздуха – в 1 см 2° С: для амплитуды температур — в 1 см 3° С; для процента суши — в 1 см 10%.
Б. Построить карту июльских и январских изотерм для Восточно-Европейской равнины. Изотермы июля (12°, 14°, 16°, 18°, 20°, 22°, 24°) провести красными линиями, изотермы января (–4°, –6°, –8°, –10°, –12°, –14°, –16°, –18°) провести синими линиями.
Изотермы проводят на контурной карте. Пользуясь атласом, находят каждый пункт на контурной карте и около него простым карандашом проставляют цифры средних температур, взятые из табл. 9 (название пункта на контурной карте писать не следует, чтобы не загружать карту; если на карте тот или иной нужный пункт не отмечен пунсоном, его нужно отметить карандашом в виде точки или кружочка).
Таблица 8.Средняя годовая температура и амплитуда температуры воздуха на разных широтах
| Полушария Земли | Показатели | Широта, град | ||||||||
| Северное | Процент суши | 43,5 | 31,5 | |||||||
| Средняя годовая температура воздуха, °С | -22,7 | -17,2 | -10,7 | -1,1 | 5,8 | 14,1 | 20,4 | 25,3 | 26,7 | 26,2 |
| Годовая амплитуда, °С | 40,0 | 32,3 | 32,1 | 29,7 | 24,9 | 18,5 | 12,5 | 5,9 | 1,8 | 1,1 |
| Южное | Процент суши | |||||||||
| Средняя годовая температура воздуха, °С | -33,1 | -27,0 | -13,6 | -3,4 | 5,8 | 11,8 | 18,4 | 22,9 | 25,3 | |
| Годовая амплитуда, °С | 34,5 | 28,7 | 19,6 | 11,2 | 5,4 | 7,1 | 8,2 | 5,8 | 3,6 |
Таблица 9.Средние температуры воздуха, ° С
| Название станции | Январь | Июль | Название станции | Январь | Июль |
| Мурманск | -11,5 | 12,6 | Казань | -13,6 | 19,9 |
| Петрозаводск | -9,6 | 16,5 | Курск | -9,3 | 19,4 |
| Санкт-Петербург | -7,9 | 17,5 | Воронеж | -9,8 | 20,6 |
| Новгород | -8,4 | 17,6 | Киев | -6,0 | 19,3 |
| Архангельск | -13,3 | 15,3 | Одесса | -3,1 | 21,4 |
| Усть-Цильма | -18,2 | 14,4 | Харьков | -7,7 | 20,6 |
| Минск | -6,8 | 17,5 | Днепропетровск | -6,0 | 22,3 |
| Нижний Новгород | -12,2 | 19,4 | Херсон | -3,4 | 23,3 |
| Москва | -10,8 | 18,0 | Ростов-на-Дону | -6,1 | 23,7 |
| Киров | -14,9 | 18,1 | Саратов | -11,3 | 23,1 |
| Пермь | -16,0 | 18,0 | Астрахань | -7,1 | 25,2 |
| Екатеринбург | -16,2 | 17,2 |
Точки с одинаковыми температурами находят методом интерполяции. Для этого ближайшие пункты соединяют прямыми линиями. Эти линии делят на части соответственно разности температур в этих двух пунктах. Затем определяют искомую точку. Все вспомогательные линии, на которых производились расчеты и цифры, обозначающие температуры пунктов, после определения точек с одинаковыми температурами стирают и проводят изотермы.
Пример.Для проведения каждой изотермы достаточно выбрать 5-7 соседних пунктов. Для построения июльской изотермы 15° выбираем следующие шесть пунктов: Мурманск, Петрозаводск, Санкт-Петербург, Новгород, Архангельск, Усть-Цильма. На карте Мурманск соединяется прямыми линиями с Петрозаводском, Санкт-Петербургом, Новгородом, Архангельском, а Архангельск – с Усть-Цильмой. Из данных таблицы видно, что между этими пунктами должны находиться точки со средней температурой июля 15° С. Далее измеряют расстояния между пунктами по проведенным прямым линиям и составляют пропорции для расчета расстояния на карте, соответствующего изменению температуры на 0,1° С. Например, измеренное расстояние между Мурманском и Санкт-Петербургом равно 15 см, а разность температур между этими пунктами в июле составляет 4,9° С.
4,9° – 15см 
Следовательно, на карте на каждые 0,3 см между Мурманском и Санкт-Петербургом температура изменяется на 0,1° С. В Мурманске средняя температура июля 12.6° С, т. е. ниже нужной нам температуры (15° С) на 2,4° С. Если на карте на каждые 0,3 см температура между Колой и Санкт-Петербургом изменяется на 0,1° С, то на 2,4° С температура изменится на расстоянии, равном:
0,1°-0,3см 
Следовательно, искомая точка с температурой 15° С будет находиться на расстоянии 7,2 см от Мурманска. Эту же точку можно найти, если расчет вести от Санкт-Петербурга.
Подобным методом определяется местоположение точек со средней температурой июля 15° С и между другими пунктами.
Для сокращения расчетов целесообразно между двумя пунктами находить сразу все требуемые точки, чтобы в последующем к этим пунктам уже не возвращаться. Так, в нашем примере между Мурманском и Санкт-Петербургом вслед за определением местоположения точки с температурой 15° С целесообразно сразу найти точки с температурой 16 и 17° С, а затем переходить к расчетам между двумя другими пунктами.
Источник