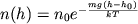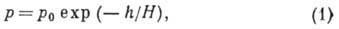Формула зависимости атмосферного давления от высоты над уровнем моря

13. Зависимость давления атмосферного воздуха от высоты, барометрическая формула (с выводом!). Графики зависимости давления и концентрации молекул от высоты при различных температурах.

Атмосферное давление — очень изменчивый метеоэлемент. Из его определения следует, что оно зависит от высоты соответствующего столба воздуха, его плотности, от ускорения силы тяжести, которая меняется от широты места и высоты над уровнем моря.1 гПа = 0,75 мм рт. ст. Или 1 мм рт. ст. = 1,333 гПа (133,322 Па).

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

где P— давление газа в слое, расположенном на высоте h — p0 давление на нулевом уровне (h=h0), M — молярная масса газа,R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

Где m — масса молекулы газа, K — постоянная Больцмана.

Вывод: Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Графики зависимости давления и концентрации молекул от высоты при различных температурах.

14. Барометрическая формула как частный случай распределения Больцмана. Нормировка распределения Больцмана. Примеры использования функции распределения Больцмана.

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА — определяет зависимость от высоты h плотности n или давления p идеального изотермического газа, находящегося в гидростатическом равновесии в однородном поле силы тяжести. Высота h отсчитывается в направлении, противоположном ускорению силы тяжести g. Б. ф. явл. частным случаем Больцмана распределения, обычно используется для описания атмосфер космич. тел (планет, звёзд). Для плотности Б. ф. можно записать в виде:

(1a)

(1б)

где n0 и p0 — плотность п давление на нек-ром начальном уровне h0, m — масса частицы газа. Иногда вместо m удобнее пользоваться молекулярной массой m = m/mu (mu- атомная единица массы), при этом в показателе степени вместо mg/kT следует писать mg/RT, где R — газовая постоянная.

Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.

Согласно распределению Больцмана среднее число частиц с полной энергией Ei равно

где Ni — кратность состояния частицы с энергией Ei — число возможных состояний частицы с энергией Ei. Постоянная Z находится из условия, что сумма ni по всем возможным значениям i равна заданному полному числу частиц n в системе (условие нормировки):

Пример: При бросании монеты на твердую горизонтальную поверхность, неясно, как она ляжет: цифрой вверх или гербом. Известно, что вероятности этих событий, при определенных условиях, равны 1/2. При бросании игральной кости нельзя с уверенностью сказать, какая из шести цифр окажется на верхней грани. Вероятность выпадения каждой из цифр при определенных предположениях (кость – однородный куб без сколотых ребер и вершин падает на твердую, гладкую горизонтальную поверхность) равна 1/6.

15. Процессы переноса: диффузия, теплопроводность, вязкость. Дифференциальные уравнения процессов переноса.

Диффузия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму.

Теплопрово́дность — это перенос тепловой энергии структурными частицами вещества (молекулами, атомами, ионами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Дифференциальные уравнения процессов переноса.

Источник

Зависимость давления от высоты: барометрическая формула

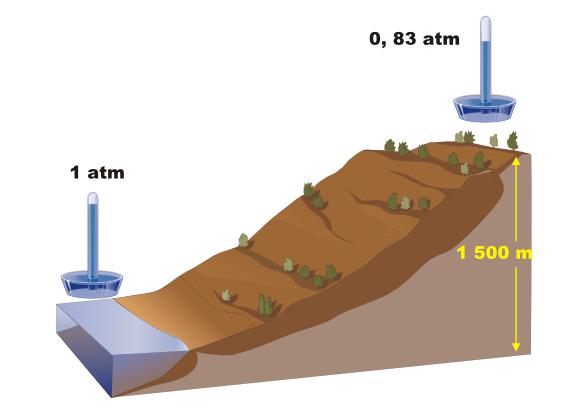
Многие люди знают, что с увеличением высоты уменьшается давление воздуха. Рассмотрим вопрос, почему давление воздуха уменьшается с высотой, приведем формулу зависимости давления от высоты, а также рассмотрим пример решения задачи с использованием полученной формулы.

Что такое воздух?

Воздух — это бесцветная смесь газов, которая составляет атмосферу нашей планеты. В его состав входят множество различных газов, основными из которых являются азот (78 %), кислород (21 %), аргон (0,9 %), углекислый газ (0,03 %) и другие.

С точки зрения физики поведение воздуха при существующих условиях на Земле подчиняется законам идеального газа — модели, согласно которой молекулы и атомы газа не взаимодействуют друг с другом, расстояния между ними огромные по сравнению с их размерами, а скорости движения при комнатной температуре составляют порядка 1000 м/с.

Давление воздуха

Рассматривая вопрос зависимости давления от высоты, следует разобраться, что представляет собой концепция «давление» с физической точки зрения. Под давлением воздуха понимают силу, с которой воздушный столб давит на поверхность. В физике она измеряется в паскалях (Па). 1 Па означает, что сила в 1 ньютон (Н) перпендикулярно приложена к поверхности площадью 1 м 2 . Таким образом, давление 1 Па — это очень маленькое давление.

На уровне моря давление воздуха составляет 101 325 Па. Или, округляя, 0,1 МПа. Это значение принято называть давлением 1 атмосферы. Приведенная цифра говорит, что на площадку 1 м 2 воздух давит с силой 100 кН! Это большая сила, однако человек ее не ощущает, так как внутри него кровь создает аналогичное давление. Кроме того, воздух относится к текучим веществам (к ним также относятся жидкости). А это значит, что он оказывает по всем направлениям одинаковое давление. Последний факт говорит о том, что давление атмосферы с разных сторон на человека взаимно компенсируется.

Зависимость давления от высоты

Атмосферу около нашей планеты держит земная гравитация. Гравитационные силы также являются виновником падения давления воздуха с увеличением высоты. Справедливости ради следует отметить, что не только земное притяжение приводит к уменьшению давления. А также снижение температуры тоже вносит свой вклад.

Поскольку воздух является текучим веществом, тогда для него можно использовать гидростатическую формулу зависимости давления от глубины (высоты), то есть ΔP = ρ*g*Δh, где: ΔP — величина изменения давления при изменении высоты на Δh, ρ — плотность воздуха, g — ускорение свободного падения.

Учитывая, что воздух является идеальным газом, из уравнения состояния идеального газа следует, что ρ = P*m/(k*T), где m — масса 1 молекулы, T — его температура, k — постоянная Больцмана.

Объединяя две приведенные выше формулы и решая полученное уравнение относительно давления и высоты, можно получить следующую формулу: P_h = P₀*e -m*g*h/(k*T) , где P_h и P₀ — давление на высоте h и на высоте уровня моря, соответственно. Полученное выражение называется барометрической формулой. Она может использоваться для расчетов зависимости атмосферного давления от высоты.

Иногда для практическим целей необходимо решать обратную задачу, то есть находить высоту, зная давление. Из барометрической формулы легко можно получить зависимость высоты от уровня давления: h = k*T*ln(P₀/P_h)/(m*g).

Пример решения задачи

Боливийский город Ла-Пас является самой «высокой» столицей в мире. Из разных источников следует, что город расположен на высоте от 3250 метров до 3700 метров над уровнем моря. Задача состоит в расчете давления воздуха на высоте Ла-Пас.

Для решения задачи воспользуемся формулой зависимости давления от высоты: P_h = P₀*e -m*g*h/(k*T) , где: P₀ = 101 325 Па, g = 9,8 м/с 2 , k = 1,38*10 -23 Дж/К, T = 293 K (20 o C), h = 3475 м (среднее между 3250 м и 3700 м), m = 4,817*10 -26 кг (с учетом молярной массы воздуха 29 г/моль). Подставляя цифры, получаем: P_h = 67 534 Па.

Таким образом, давление воздуха в столице Боливии составляет 67 % от давления на уровне моря. Низкое давление воздуха является причиной головокружений и общей слабости организма, когда человек поднимается в горные районы.

Источник

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА

(от греч. baros — тяжесть и metreo — измеряю) — формула, определяющая зависимость давления от высоты в поле силы тяжести. Б. ф. для атмосферы Земли следует из ур-ния гидро-статич. равновесия и состоит в том, что в изотермич. случае давление атмосферы р экспоненциально уменьшается с высотой h:

где р 0 — давление у поверхности Земли, шкала высот определяется темп-рой T и средним молекулярным весом — масса атома водорода, g — ускорение силы тяжести. Б. ф. в виде (1) справедлива лишь при неизменной темп-ре и только для стабильных частиц атмосферы.

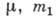
Для реальных условий Б. ф. (1) требует нек-рого уточнения.

1) Поскольку T непостоянна по высоте (в тропопаузе на высоте 10-17 км и в мезопаузе на высоте 80 км находятся минимумы T, в стратопаузе на высоте 50 км — максимум, а в термосфере на высотах 80-250 км T растёт), а на больших высотах изменяется и , то величину h/H следует заменить величиной .

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Источник