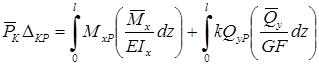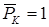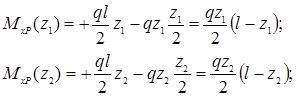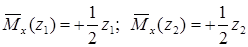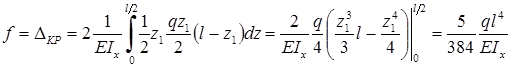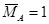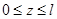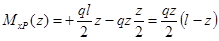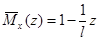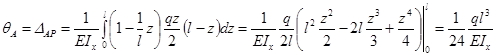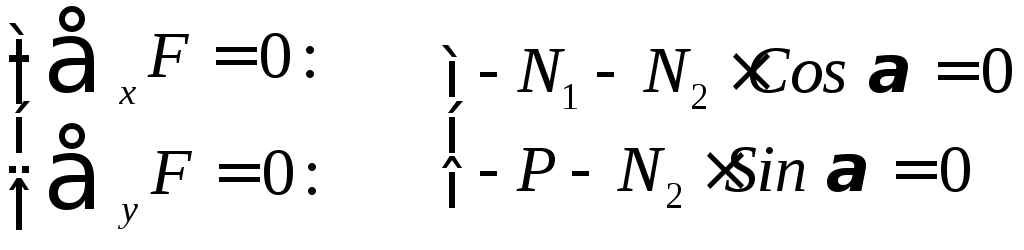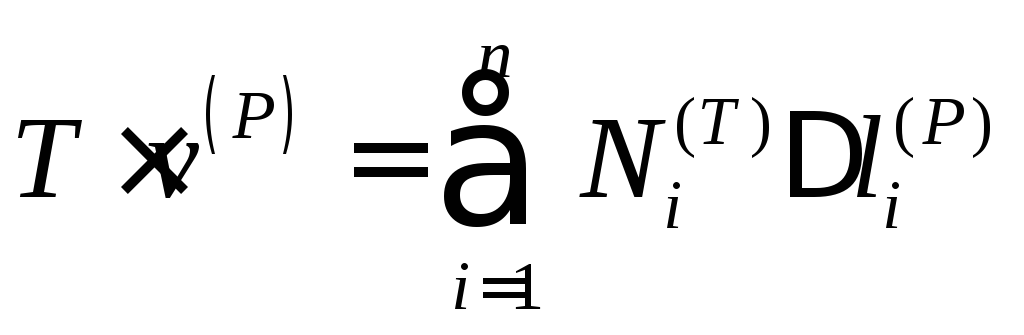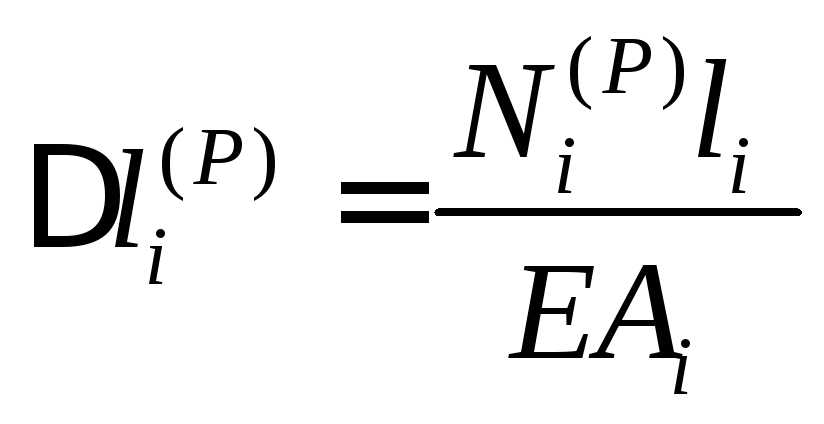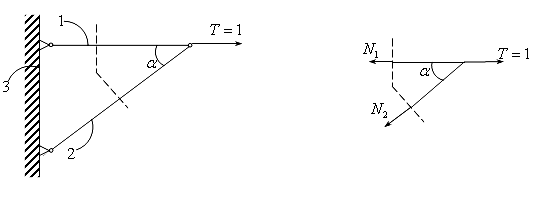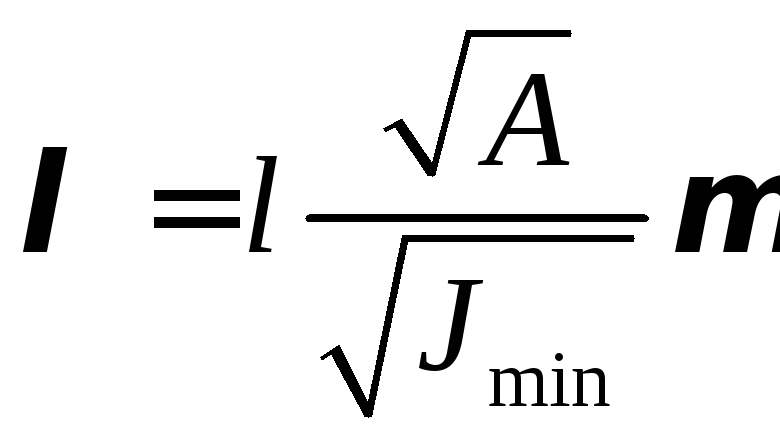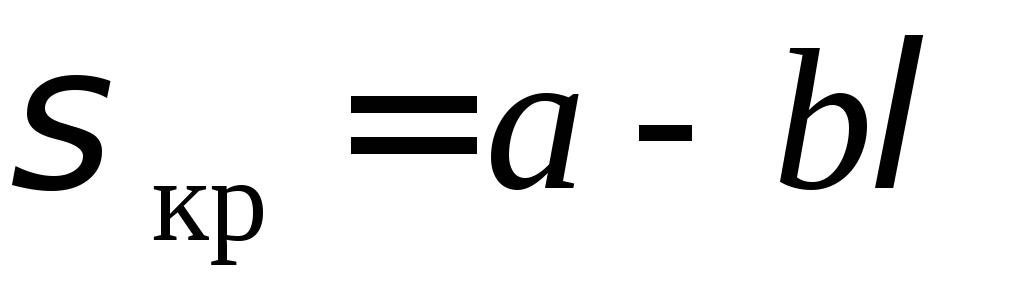Формула мора для прогиба фермы

Ключевые слова: ферма, индукция, Maple, прогиб, интеграл Мора.

Фермы балочного типа широко применяются в строительстве и машиностроении как основные и вспомогательные несущие конструкции. Одной из важнейших характеристик фермы является ее жесткость. Простейшие модели ферм имеют шарнирное крепление стержней, обеспечивающее статическую определимость. Несмотря на это, непосредственный расчет усилий в таких фермах не всегда возможен. Особенно это касается ферм шпренгельного типа, где метод сечений не работает. Численные расчеты в стандартных программах для определения напряженно-деформированного состояния фермы с увеличением числа панелей могут давать погрешности за счет накопления ошибок округления. В любом случае, простые формулы для расчета прогиба всегда полезны, однако не всегда такие формулы настолько универсальны, чтобы не просто тестировать численные решения, но и позволять проводить качественный анализ конструкций математическими методами. В частности, как правило, простые формулы для расчета прогиба не учитывали конфигурацию решетки (формула Качурина [1,2]) и выводились на основе моделирования балочной фермы путем замены ее на балку такой же жесткости. С появлением систем компьютерной математики появилась возможность вывода точных формул для прогиба ферм с любым числом панелей, что исключает эффект накопления ошибок округления. Наряду с методом непосредственного расчета фермы с параметрическим заданием числа панелей [3] в тех случаях, когда для расчета усилий в стержнях можно использовать метод сечения и метод поэтапного вырезания узлов, для вывода аналитических решений применяется метод индукции. Этим методом были получены формулы для прогиба плоских ферм арочного типа 5, рам 9, решетчатых ферм с различными схемами решеток 14 и некоторых регулярных пространственных ферм 21. Метод применим и для частотного анализа стержневых конструкций 30. В настоящей работе приводится вывод формул прогиба для балочной фермы шпренгельного типа (рис. 1).

Схема фермы и расчет усилий

Верхний пояс фермы, подверженный сжатию, состоит из укороченных стержней длиной a . Это обеспечивает больший запас устойчивости конструкции. В ферме n =2 k панелей. ________________ © Суд И. Б., 2020 26

Каждая панель состоит из двух стержней верхнего пояса, стержня нижнего пояса длиной 2 a , стойки высотой f и четырех раскосов. Общая высота фермы f+h . Средняя стойка имеет высоту h+f . Расчет прогиба конструкции начинается с определения усилий в стержнях. Используется программа, составленная для решения данной задачи в системе символьной математики Maple.

Рис. 1. Ферма под действием равномерной нагрузки, k =4

Стержни и узлы фермы нумеруются (рис. 2). Координаты шарниров вводятся в циклах. На языке Maple это имеет вид: > for i to 2*n+1 do x[i]:=(i-1)*a; y[i]:=h+f; od: > for i to n+2 do x[i+2*n+1]:=(i-1)*2*a-a; y[i+2*n+1]:=h; od: > for i to n+1 do x[i+3*n+3]:=(i-1)*2*a; y[i+3*n+3]:=0; od:

Рис. 2. Нумерация узлов и стержней, n =4

Схема решетки в программе задается специальными упорядоченными списками N[i] номеров концов соответствующих стержней. Выбор начала и конца стержня не влияет на величину усилия или его знак. Ввод решетки напоминает задание графа в дискретной математике: for i to 2*n do N[i]:=[i,i+1];od: for i to n do N[i+2*n]:=[3*n+3+i,i+3*n+4]; N[i+7*n+4]:=[2*n+2+i,2*i]; od: for i to n+1 do N[i+3*n]:=[2*i-1,i+2*n+1]; N[i+4*n+1]:=[2*i-1,i+2*n+2]; N[i+5*n+2]:=[i+3*n+3,i+2*n+2]; N[i+6*n+3]:=[i+3*n+3,i+2*n+1]; od: N[8*n+5]:=[n+1,3*n+k+4]: 27

По данным координат и номеров концов стержней составляется матрица системы уравнений равновесия узлов. Решение системы одновременно дает и усилия в стержнях и реакции опор (с обратным знаком). Значения усилий используются в интеграле Мора

стержнях от действия внешней нагрузки,	s		j	–	усилия от безразмерной единичной силы,
	приложенной к узлу в середине пролета,	l				j	–	длина стержня с номером j . Три опорных

стержня, принятые жесткими, в сумму не входят (бесконечная жесткость).

Прогиб

Расчет ряда ферм с разным числом панелей показал, что итоговая формула для прогиба имеет один и тот же вид, не зависящий от числа панелей. При действии распределенной нагрузки имеем

3	h C	a	3	f C	( g	3	3	) f C	f	2	2	)
EF P ( C a			c			4	h ( h f )) / (2 f ( h f )			,
1	2	3

где коэффициенты формулы зависят только от числа k панелей в половине пролета. Методом индукции, обработкой серии решений для 14 ферм, получаем следующие коэффициенты:

C ( 2 k

2

2( 1)

k

k

2 k ( 1)

k

1) / 2

,

1

C

(40k 4

80k 3 62k 2

6( 1) k k 22k 3( 1) k 3) / 6 ,

2

C

(4 k

2

4 k 1) / 2

,

C

( 1)

k

.

4

3

Рекуррентное уравнение для коэффициента C 1

, полученное оператором rgf_findrecur,

имеет вид: C 1,k C 1,k 1 2C 1,k 2 2C 1,k 3 C 1,k 4 C 1,k 5 .

Уравнение для коэффициента C 2							имеет вид
C	2, k	3 C	2, k 1	C	2, k 2	5 C		5 C	C	3 C	C
2, k 3		2, k 4		2, k 5		2, k 6	2, k 7
Уравнение для коэффициента C 3							:
C 3,k 3C 3,k 1 3C 3,k 2 C 3,k 3 .

Самым простым уравнением оказалось уравнение для коэффициента

C

4, k

C

4, k 1 .

Прогиб в случае сосредоточенной в середине ожидать, имеет более простой вид:

EF	( C a	3	C	( g	3	3	) 2( f	2	h
		c
1	2
где C (16k 3	24k 2	8k) / 3	, C	2 k 1.
1	2

Проанализируем полученное решение в случае действия распределенной нагрузки. Построим графики зависимости относительного прогиба ‘ EF / ( P 0 L ) , где P P 0 / (2 n 1) от высоты h при фиксированной высоте f+h =10 м для разного числа панелей k . Фиксируем пролет фермы L= 2( n+ 1) = 70 м (рис. 3). Рис. 3 . Зависимость прогиба от высоты h при разном числе панелей k , h + f = 10 м, L=70 м. 1 – k= 3; 2 – k= 4; 3 – k= 5 Интересно отметить сильную зависимость решения от числа панелей. Минимум прогиба во всех трех случаях наблюдается при одинаковых размерах f=h . При небольшом числе панелей и, следовательно, достаточно длинных стержнях поясов, наибольшая жесткость наблюдается при больших значениях h и малых значениях f . Зависимость прогиба от числа панелей, при разных h , представлена кривыми на рис. 4. На первый взгляд проявляется устойчивая тенденция к уменьшению прогиба с ростом k . Однако асимптотика решения линейна и положительна:

lim ‘/ k ( f 2	hf h 2 ) / (2(h f )L)
k

Рис. 4 . Зависимость прогиба от числа панелей k при разной высоте h, f= 3 м, L=70 м . 1—h= 1 м; 2—h= 1.5 м; 3—h= 2 м. 29

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

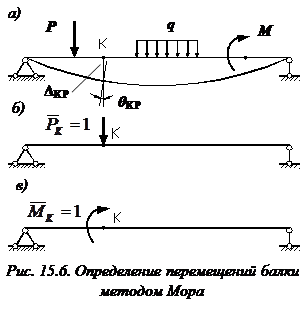
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

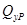
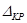
Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

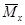
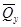
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

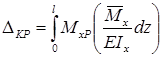
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

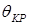
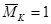
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

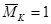
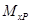
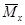
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

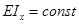
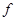
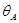
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

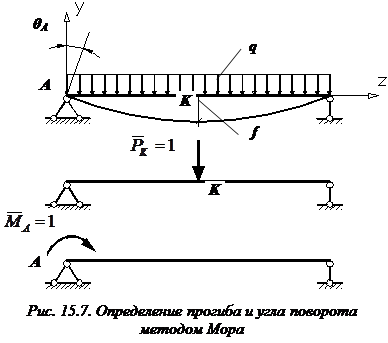
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

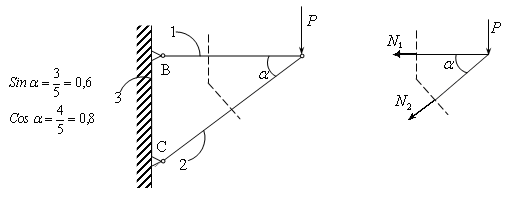
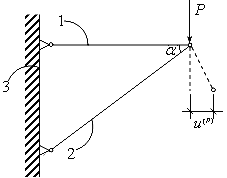
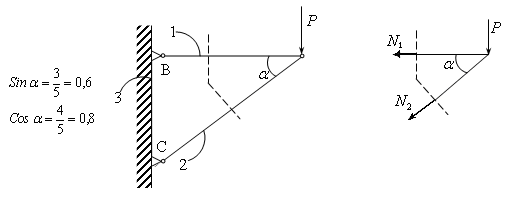
7. Метод сечений для вычисления сил растяжения (на примере фермы из двух стержней) .

Рассечем конструкцию на 2 части и запишем условия равновесия правой части:

Отсюда, находим , .

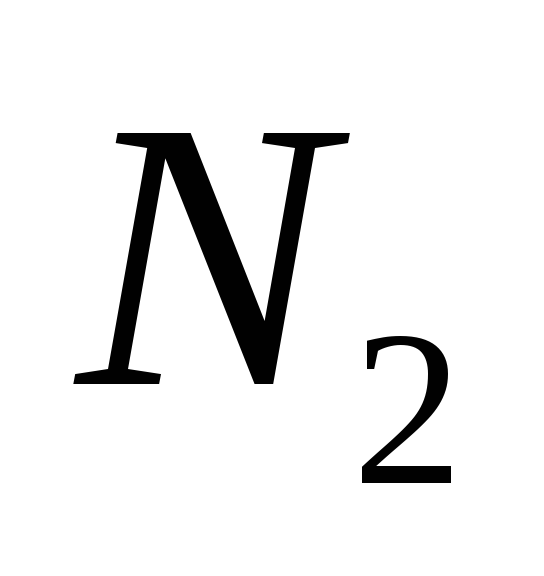
8. Закон сохранения энергии и формула Мора для вычисления перемещений точек фермы

Согласно закону сохранения, никакая работа не исчезает, она тратится на совершение другой работы или переходит в другую энергию. Согласно этому закону формулу Мора можно записать в виде:

— искомое перемещение,

— удлинения стержней, которые появляются под действием внешних рабочих нагрузок:

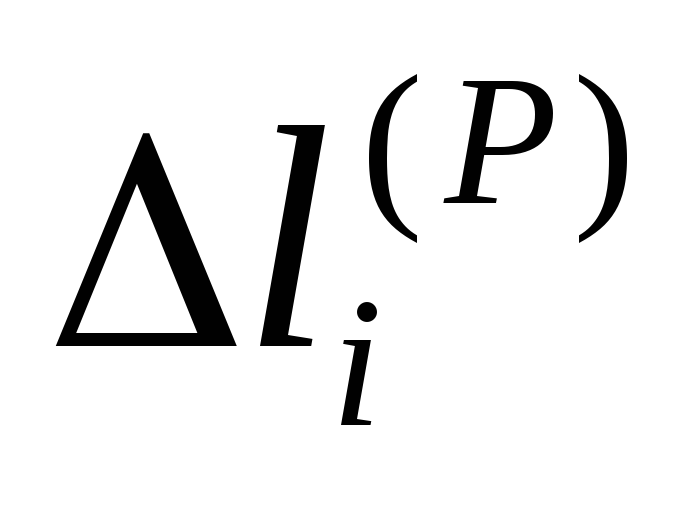
Задача о действии рабочих нагрузок изображена на рисунке:

— усилия растяжения стержней, которые возникают от действия единичной силы Т , которая приложена в интересующей нас точке и в направлении . Задача о действии единичной силыТ изображена на рисунке:

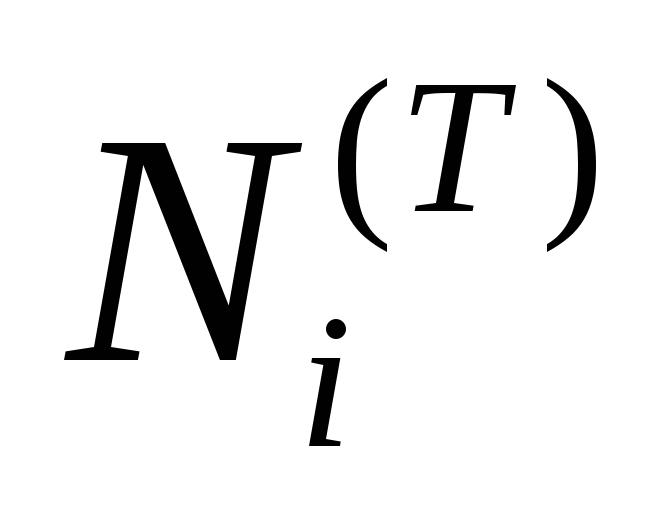
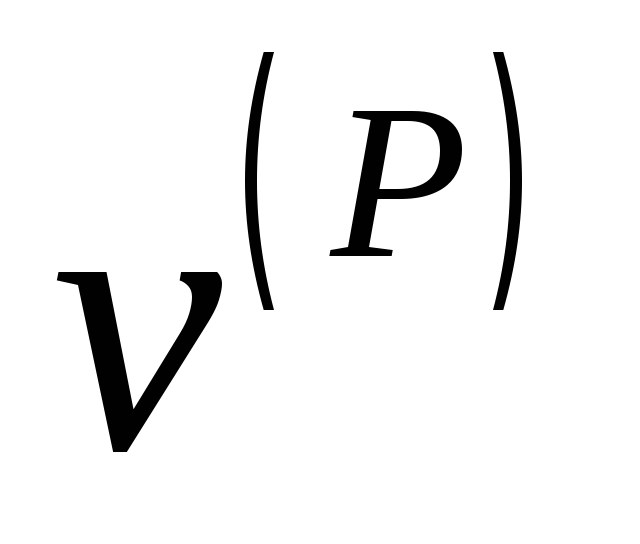
Устойчивость сжатых стержней

9. Что значит потеря устойчивости, что такое критическая сила, критическое напряжение, гибкость, коэффициент приведенной длины?

Рассмотрим сжатый стержень. При некотором значении Р происходит резкая смена прямолинейной формы в криволинейную при малейшем поперечном воздействии. Это явление называется потерей устойчивости.

Сила Р_кр, при которой это происходит, называется критической, а соответствующее ей напряжение называют критическим напряжением:

.

Гибкость — это относительная длина стержня (безразмерная величина):

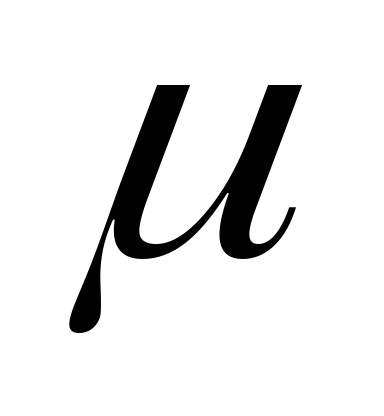
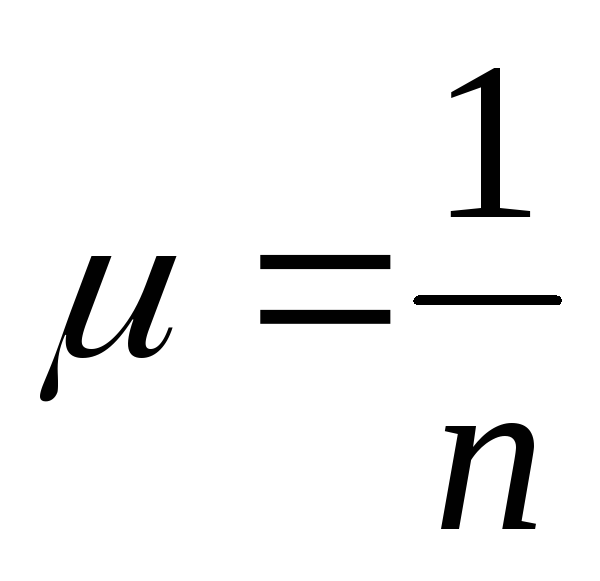
Здесь — коэффициент приведенной длины (вычисляется через число волн, образующихся при изгибе):.

10. Формулы Эйлера и Ясинского и области их применения (с пояснениями параметров, входящих в них).

Формула Эйлера: , гдегибкость стержня,Е — модуль Юнга.

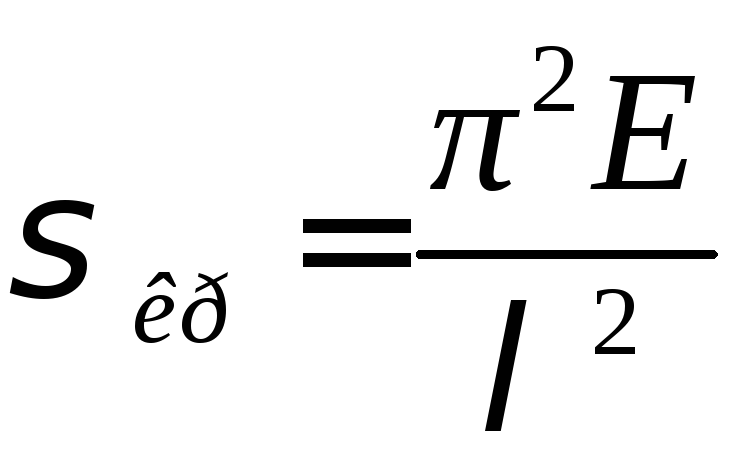
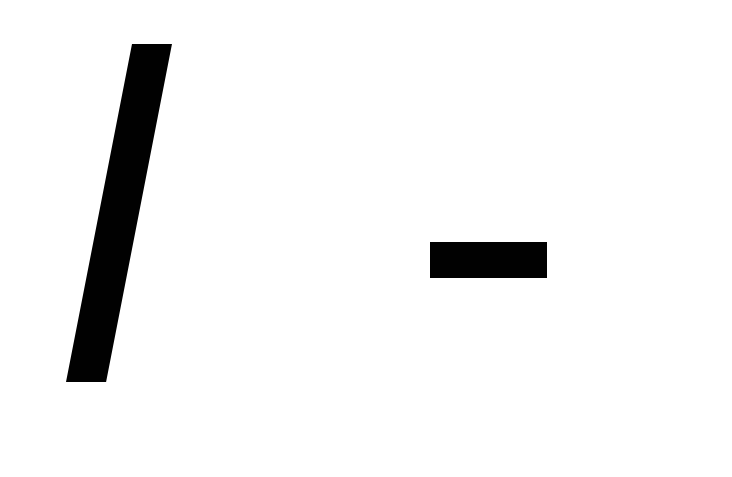
Ее нужно применять для тех стержней, у которых после вычислений

получится 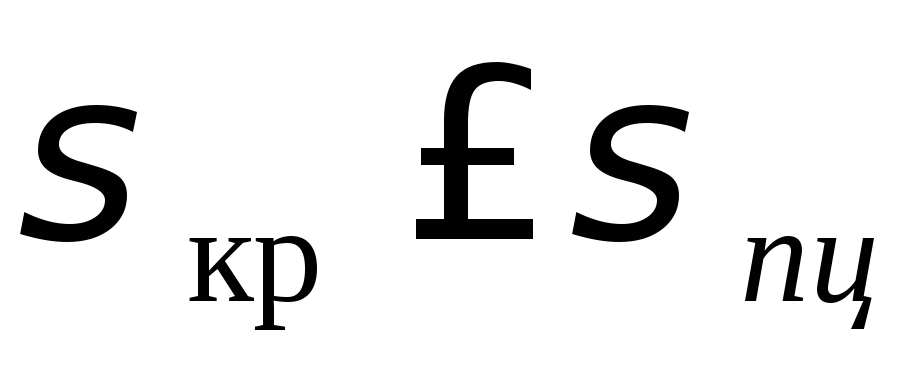(для стали это условие обеспечивается, если).

Такие стержни называются длинными

Формула Ясинского: (а и b — постоянные, зависящие от материала).

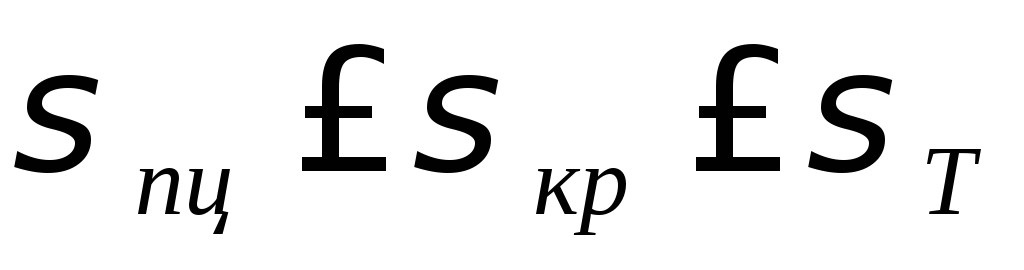
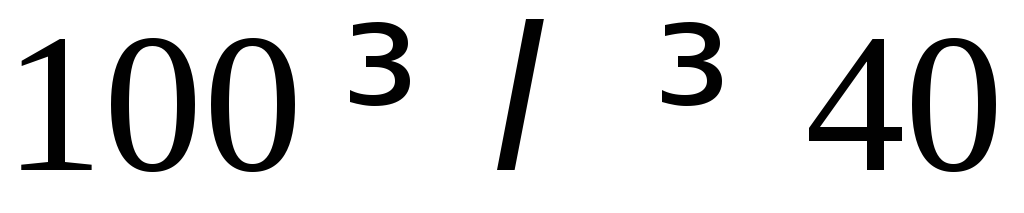
Ее нужно применять для тех стержней, у которых после вычислений получится (для стали это условие обеспечивается, если). Такие стержни называютсястержнями средней длины

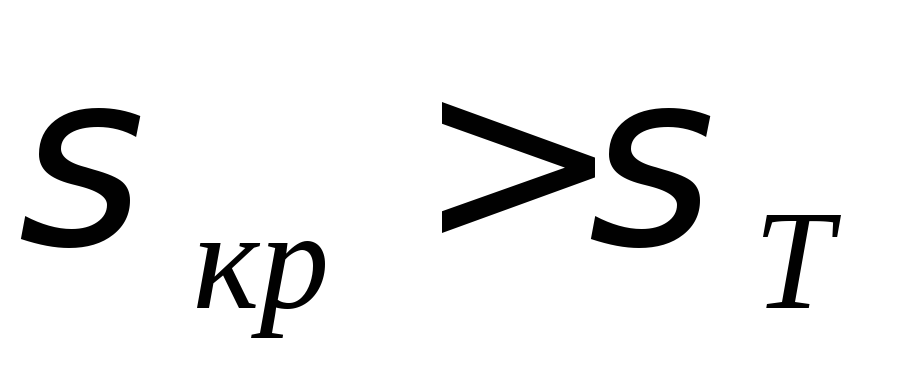
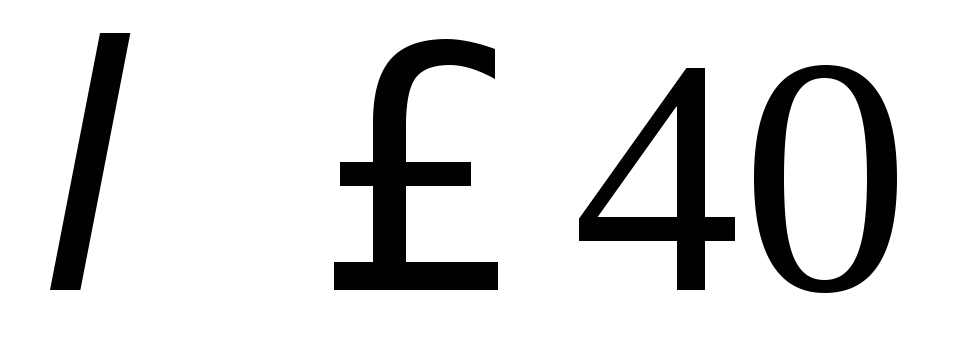
Короткие стержни – это стержни, которые не теряют устойчивость, для них и по формуле Эйлера, и по формуле Ясинского получится (для стали это условие обеспечивается, если ).

12. Что такое поперечная сила, изгибающий момент?

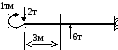
Рассечем брус на две части. Суммарная сила, с которой левая часть бруса воздействует на правую поперек оси бруса, называется поперечной силой Q_y . Например, в сечении на расстоянии 3 м. Q_y = -2т. (См. рисунок)

Суммарный момент, с которым левая часть бруса воздействует на правую относительно оси, поперечной брусу (относительно оси х), называется изгибающим моментом М_х. Например, в сечении на расстоянии 3 м.

М_х = -2т∙3м.+1т∙м. (См. рисунок)

13. Формула Навье для вычисления нормальных напряжений σ при изгибе ( с пояснениями параметров, входящих в нее).

Здесь Jx — момент инерции, у – расстояние от нейтральной линии 0х до точки в которой вычисляется напряжение

Источник