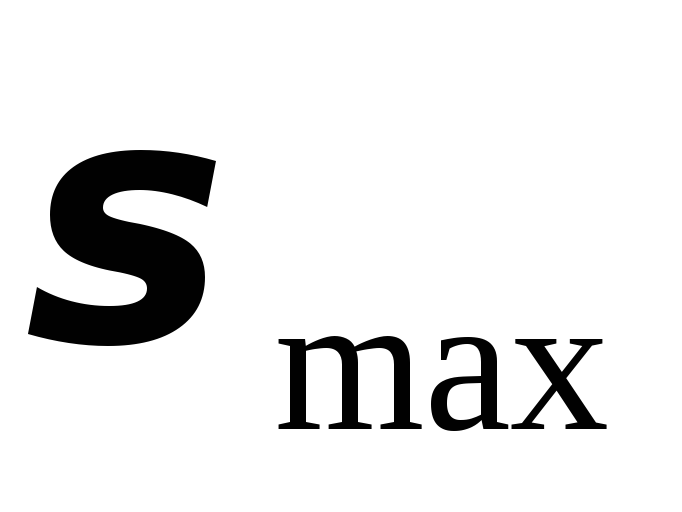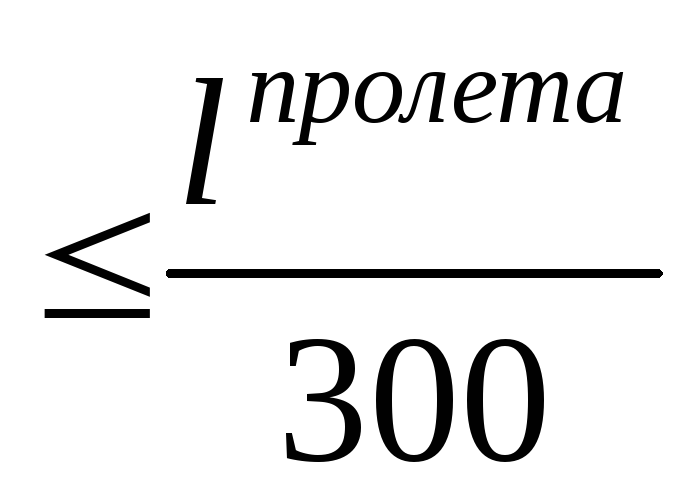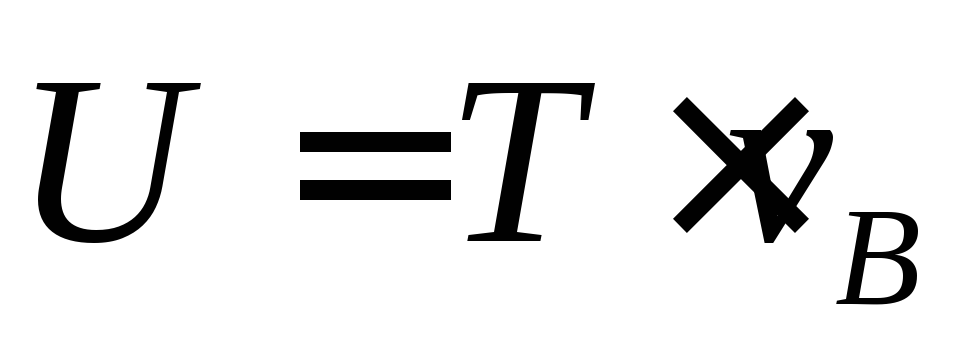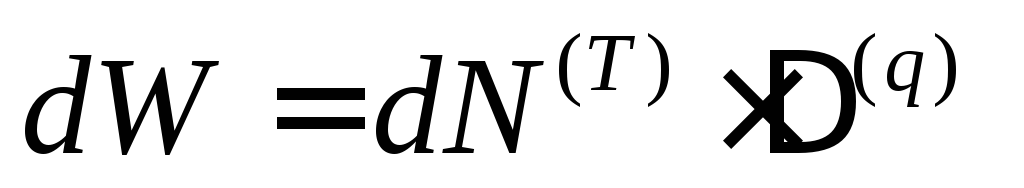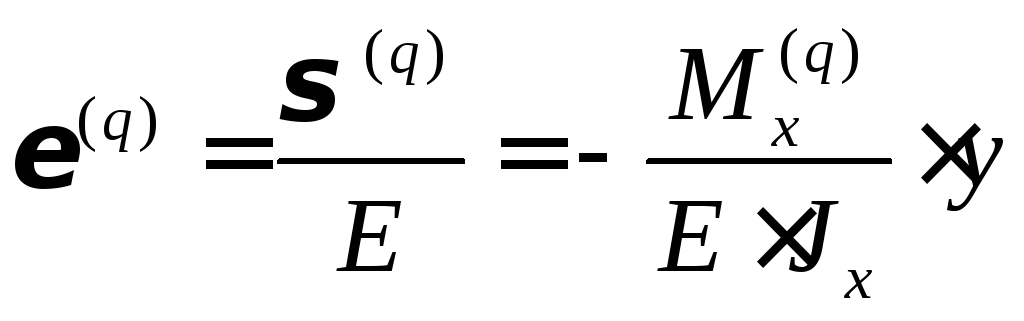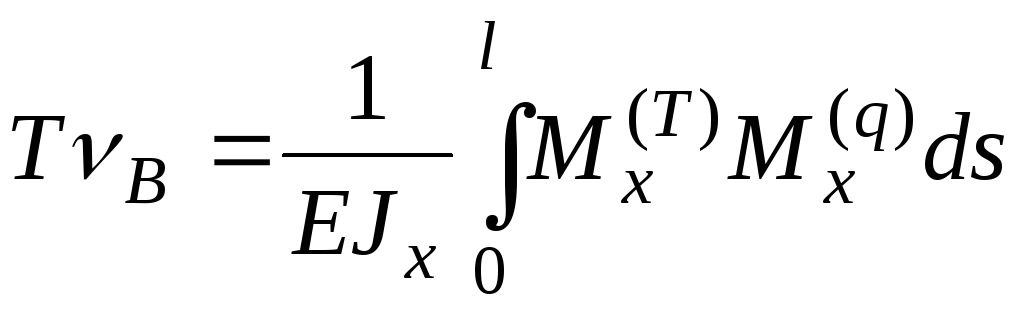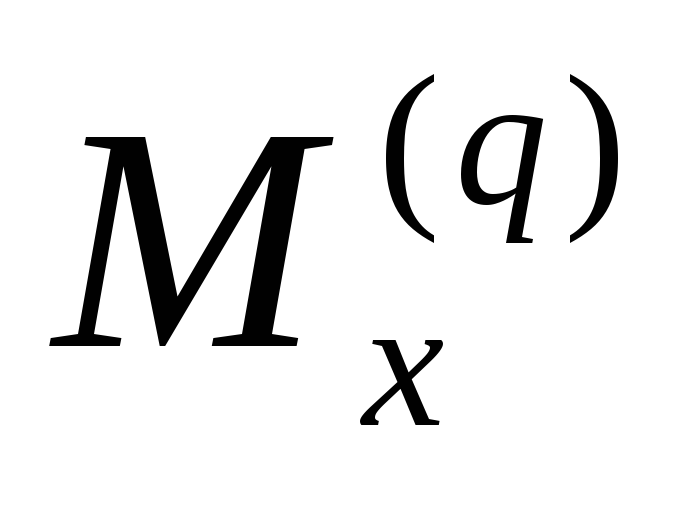Формула Мора для вычисления прогиба
Для решения задачи используем применим закон сохранения энергии в варианте принципа возможных перемещений. В качестве возможных выберем прогиб (здесь и далее величины, характеризующие основную задачу будут снабжаться индексом q).
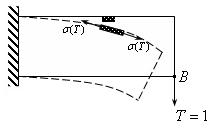
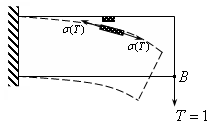
Рассмотрим фиктивную задачу (рис.16.3)
Вычислим работу силы на перемещении :
Согласно закона сохранения энергии эта работа должна равняться работе внутренних сил. Подсчитаем её.
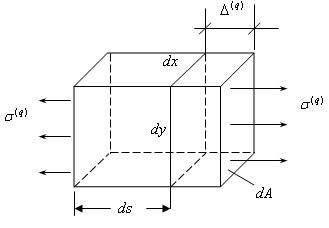
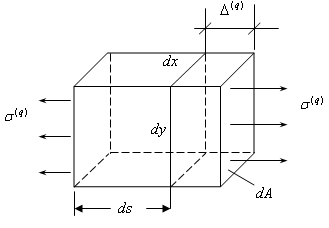
Рассмотрим рис.16.2 и рис.16.3. Выделим малый элемент балки (он зачернен на рис 16.2 и рис.16.3). Он удлиняется на величину .
Рассмотрим этот же малый элемент под действием напряжений растяжения (здесь и далее величины, характеризующие фиктивную задачу, будут снабжаться индексом Т), которые возникают, под действием силы Т. Вычислим — работу этих напряжений на перемещении :
Здесь – объем малого элемента.
Работа по удлинению всех элементов балки будет:
Запишем закон сохранения энергии:
Отсюда вытекает формула Мора:
Здесь — искомый прогиб в точке B (от рабочих нагрузок);
=1 – единичная сила, приложенная в интересующем нас направлении искомого прогиба в интересующей нас точке В.
— изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.
— изгибающий момент от рабочих нагрузок.
Физический смысл формулы Мора заключается в следующем: работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.
1. Работой касательных напряжений обычно пренебрегают ввиду ее малости по сравнению с W.
2. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид
Источник
4. Расчет по III и IV теориям прочности.
Балки из пластических материалов, имеющих одинаковые пределы текучести при растяжении и сжатии проверяют по III или IV теориям прочности.
Согласно третьей теории условие прочности имеет вид:


Это условие называется условием прочности балки по третьей теории прочности
Аналогично можно записать условие прочности по четвертой теории:


В этих последних двух случаях также необходимо строить эпюры 
1. Для стандартных двутавров, в большинстве случаев 

2. Видно, что четвертая теория является более экономичной, т.е. третья теория дает больший запас прочности при расчете балок. Для стали четвертая теория лучше коррелирует с экспериментом.
16. Расчет балки на жесткость
Балка называется жесткой, если для заданных (рабочих, проектных) нагрузок она прогибается в пределах нормы (норму устанавливает заказчик)
Часто в строительстве принимаются следующие условия:
В пролете прогиб должен быть (16.1)
На консоли прогиб должен быть
Обозначение: Прогиб принято обозначать буквой
Основная трудность проверки жесткости — это вычисление прогибов. Методов их вычисления достаточно много.
16.1. Формула Мора для вычисления прогиба
Пусть необходимо найти прогиб точки В, т.е. перемещение vB.(рис.16.2)
Для решения задачи используем применим закон сохранения энергии в варианте принципа возможных перемещений. В качестве возможных выберем прогиб (здесь и далее величины, характеризующие основную задачу будут снабжаться индексомq).
Рассмотрим фиктивную задачу (рис.16.3)
Вычислим работу силы 

.
Согласно закона сохранения энергии эта работа должна равняться работе внутренних сил. Подсчитаем её.
Рассмотрим рис.16.2 и рис.16.3. Выделим малый элемент балки (он зачернен на рис 16.2 и рис.16.3). Он удлиняется на величину .
Рассмотрим этот же малый элемент под действием напряжений растяжения 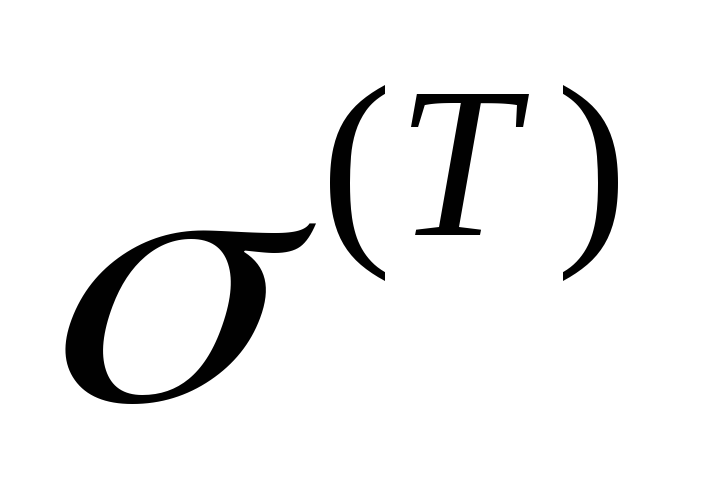


Здесь – объем малого элемента.
Работа по удлинению всех элементов балки будет:
.
.
.
Запишем закон сохранения энергии:
Отсюда вытекает формула Мора:
(16.2)
Здесь — искомый прогиб в точкеB (от рабочих нагрузок);

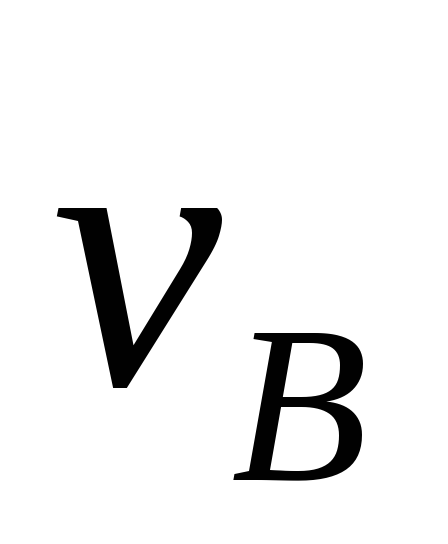
— изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.
— изгибающий момент от рабочих нагрузок.
Физический смысл формулы Мора заключается в следующем: работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.
1. Работой касательных напряжений обычно пренебрегают ввиду ее малости по сравнению сW.
2. При необходимости вычисления угла наклона балкиα вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид
.
Источник
4. Расчет по III и IV теориям прочности.
Балки из пластических материалов, имеющих одинаковые пределы текучести при растяжении и сжатии проверяют по III или IV теориям прочности.
Согласно третьей теории условие прочности имеет вид:
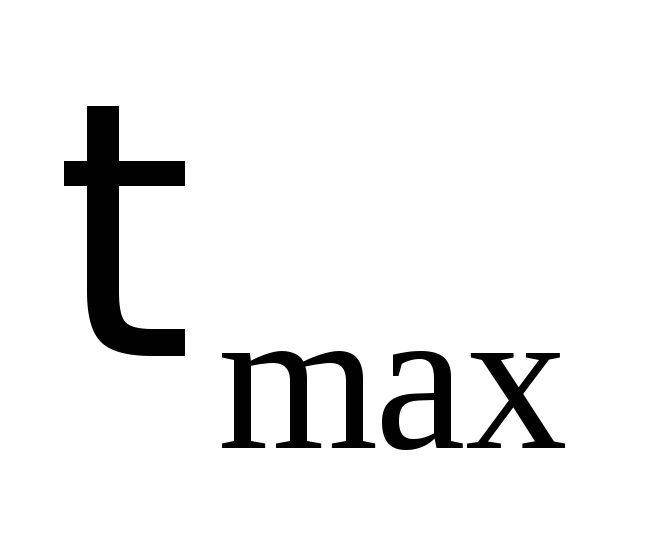

Это условие называется условием прочности балки по третьей теории прочности
Аналогично можно записать условие прочности по четвертой теории:


В этих последних двух случаях также необходимо строить эпюры 
1. Для стандартных двутавров, в большинстве случаев 

2. Видно, что четвертая теория является более экономичной, т.е. третья теория дает больший запас прочности при расчете балок. Для стали четвертая теория лучше коррелирует с экспериментом.
16. Расчет балки на жесткость
Балка называется жесткой, если для заданных (рабочих, проектных) нагрузок она прогибается в пределах нормы (норму устанавливает заказчик)
Часто в строительстве принимаются следующие условия:
В пролете прогиб должен быть (16.1)
На консоли прогиб должен быть
Обозначение: Прогиб принято обозначать буквой
Основная трудность проверки жесткости — это вычисление прогибов. Методов их вычисления достаточно много.
16.1. Формула Мора для вычисления прогиба
Пусть необходимо найти прогиб точки В, т.е. перемещение vB.(рис.16.2)
Для решения задачи используем применим закон сохранения энергии в варианте принципа возможных перемещений. В качестве возможных выберем прогиб (здесь и далее величины, характеризующие основную задачу будут снабжаться индексомq).
Рассмотрим фиктивную задачу (рис.16.3)
Вычислим работу силы 

.
Согласно закона сохранения энергии эта работа должна равняться работе внутренних сил. Подсчитаем её.
Рассмотрим рис.16.2 и рис.16.3. Выделим малый элемент балки (он зачернен на рис 16.2 и рис.16.3). Он удлиняется на величину .
Рассмотрим этот же малый элемент под действием напряжений растяжения 
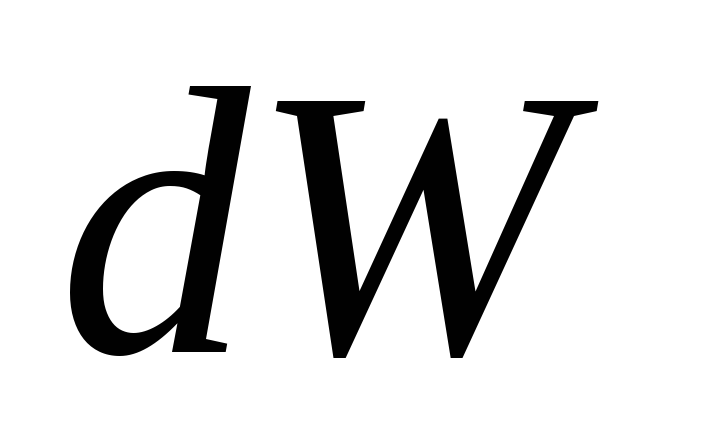
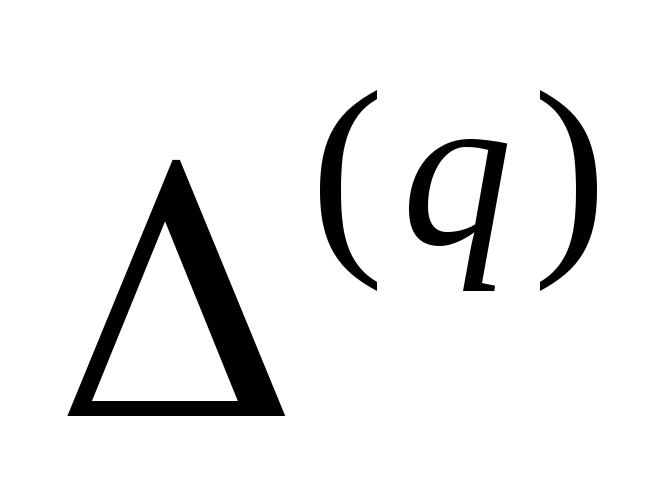
Здесь – объем малого элемента.
Работа по удлинению всех элементов балки будет:
.
.
.
Запишем закон сохранения энергии:
Отсюда вытекает формула Мора:
(16.2)
Здесь — искомый прогиб в точкеB (от рабочих нагрузок);


— изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.
— изгибающий момент от рабочих нагрузок.
Физический смысл формулы Мора заключается в следующем: работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.
1. Работой касательных напряжений обычно пренебрегают ввиду ее малости по сравнению сW.
2. При необходимости вычисления угла наклона балкиα вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид
.
Источник