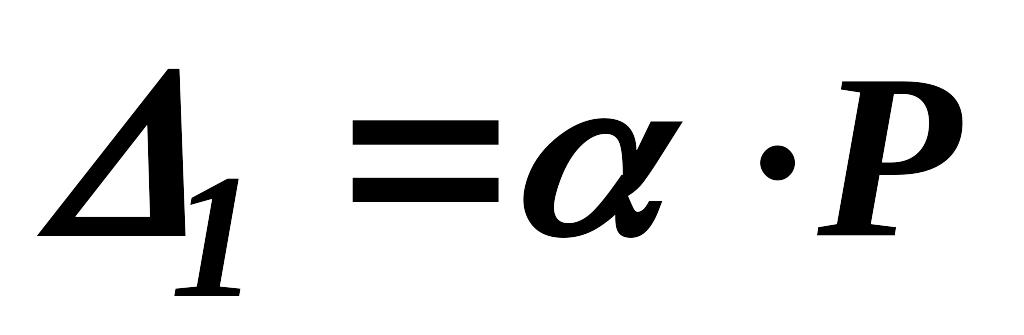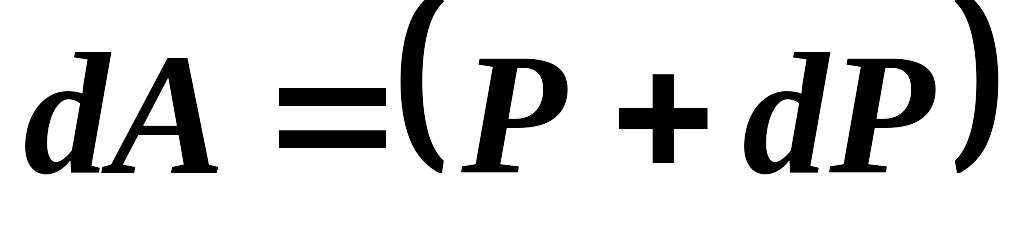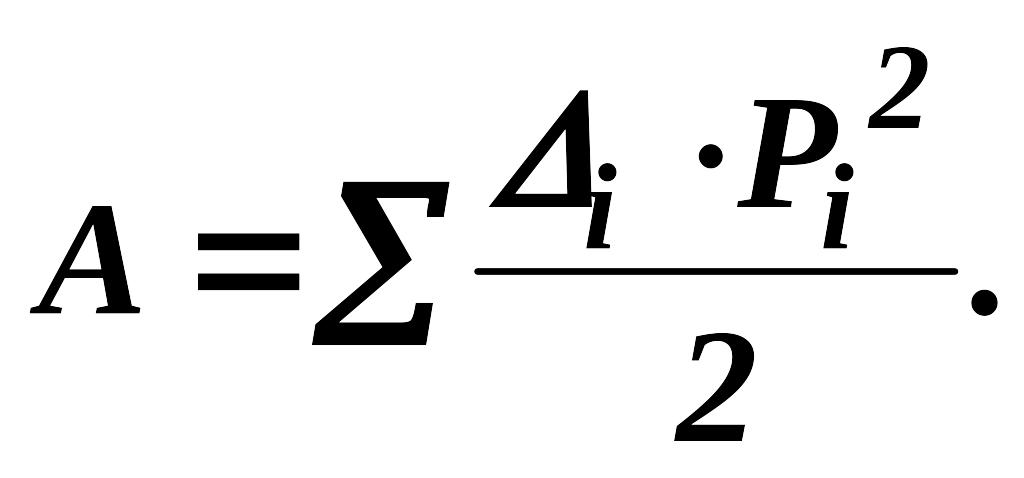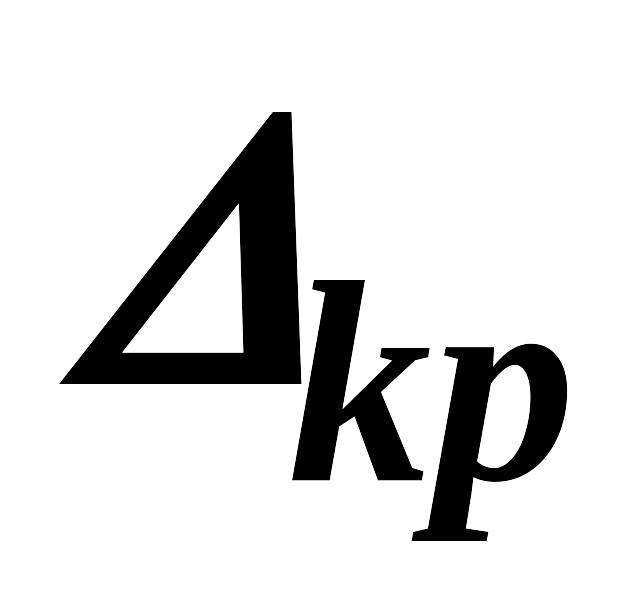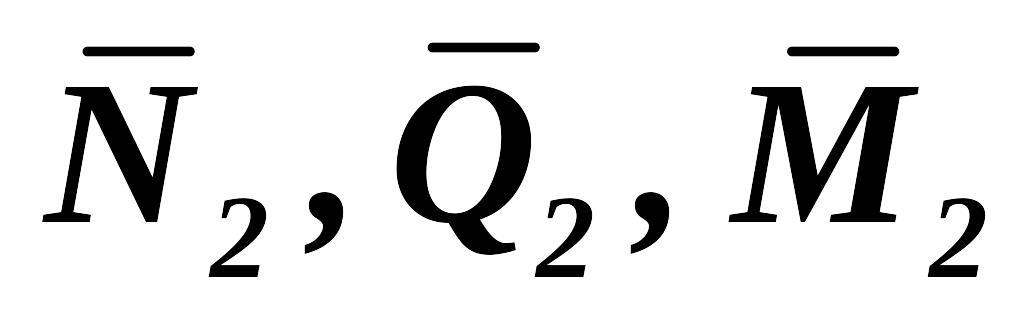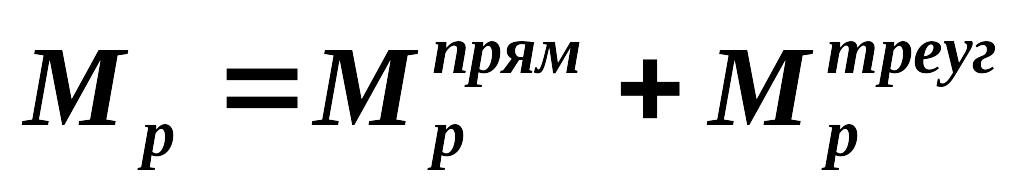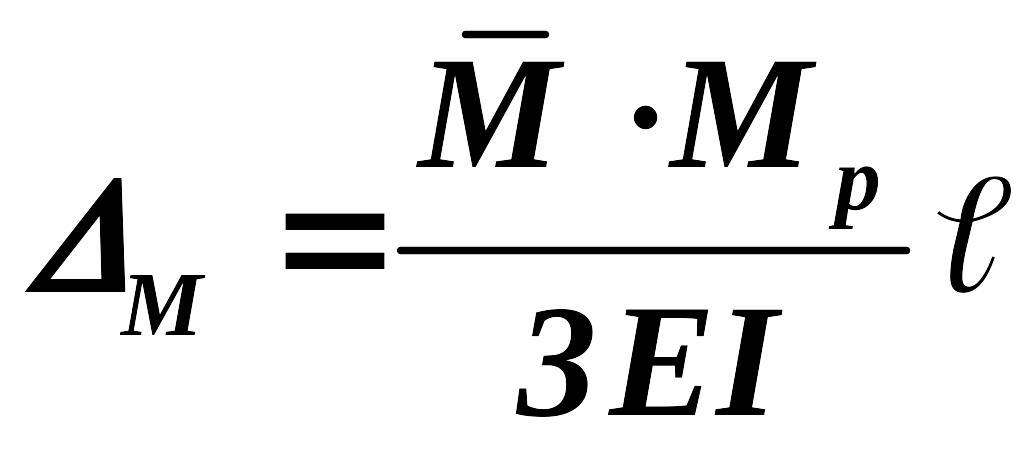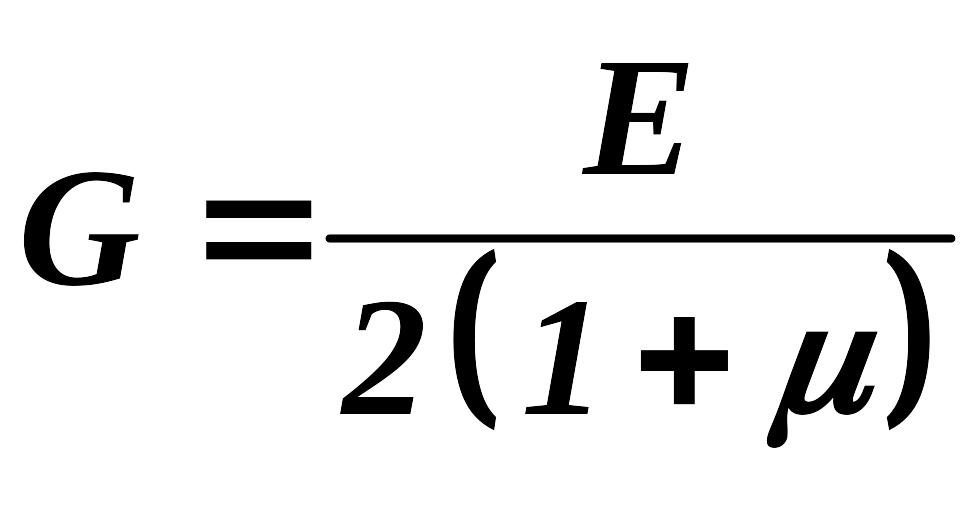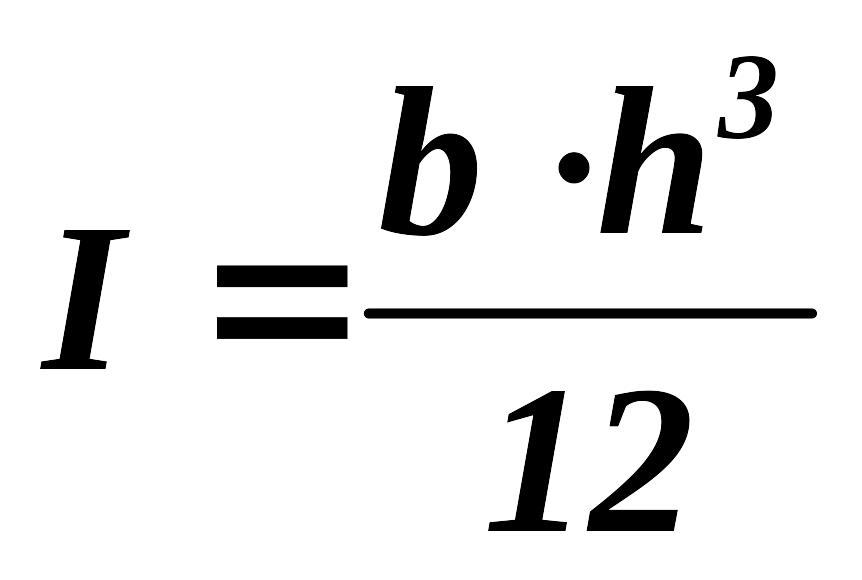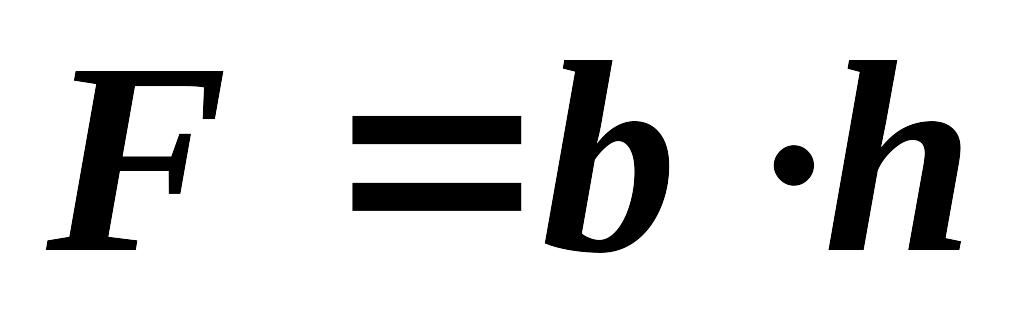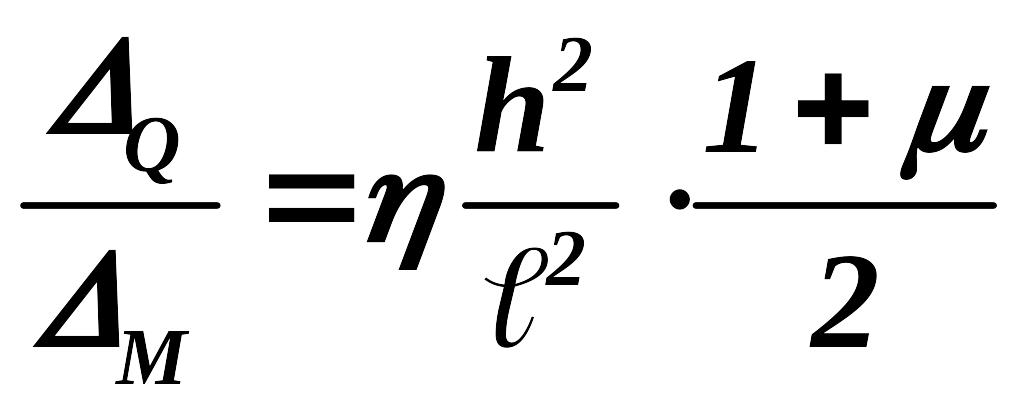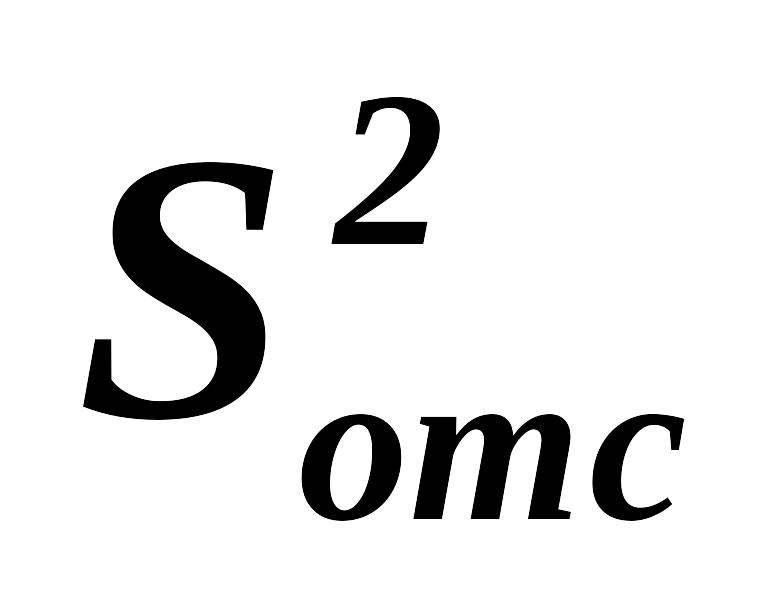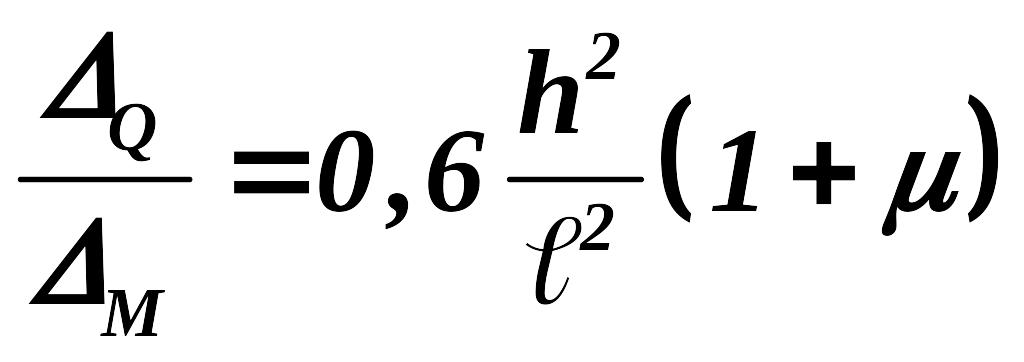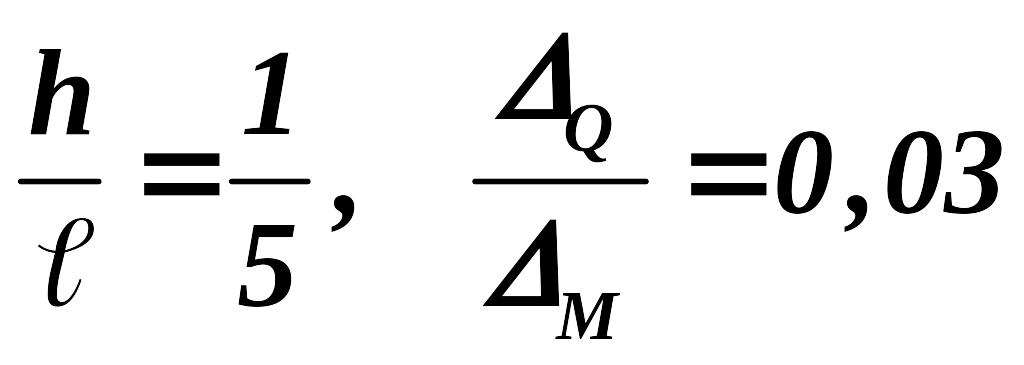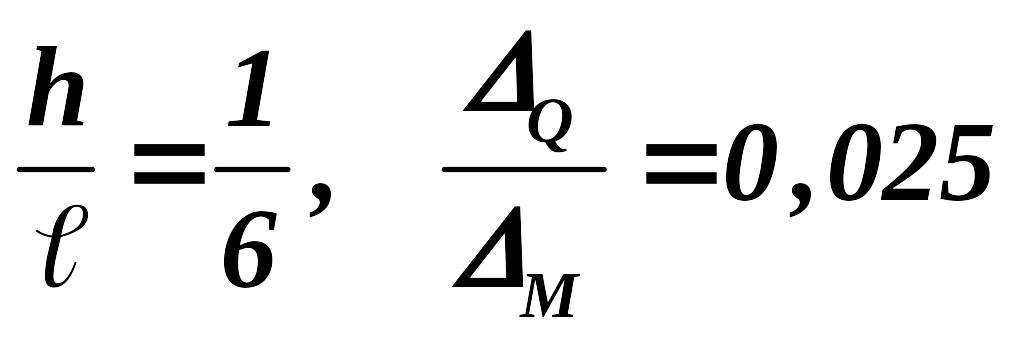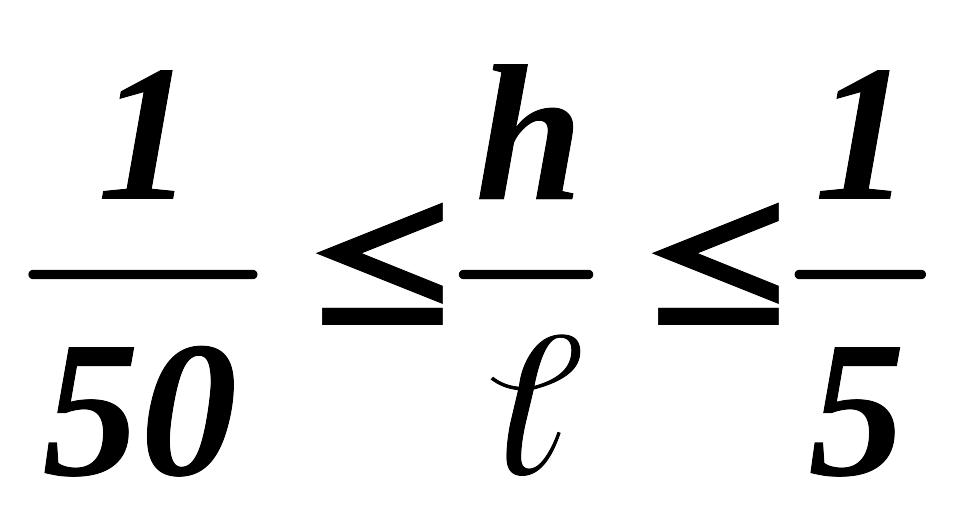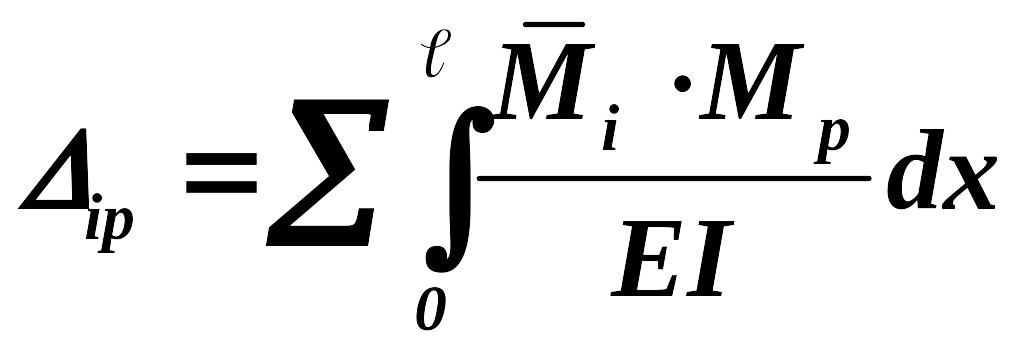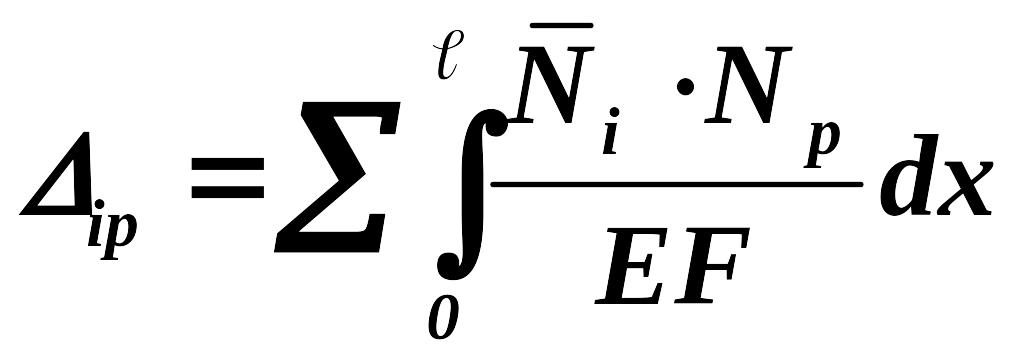Метод Максвелла – Мора определения перемещений
Метод Максвелла – Мора определения перемещений является универсальным методом, справедливым, в отличие от рассмотренного выше аналитического способа, не только для балок, но и для любых стержневых систем. Чтобы понять сущность метода Максвелла – Мора, введем понятия обобщенной силы и обобщенного перемещения [2]. Обобщенной силой называется любое однопараметрическое силовое воздействие: это может быть и сосредоточенная сила, и сосредоточенный момент, и распределенная нагрузка, и группа сил, связанных между собой. Обобщенным перемещением, соответствующим заданной обобщенной силе, называется то перемещение, на котором обобщенная сила совершает работу. Приведем два самых важных для практики примера. Если обобщенной силой (о.с.) является вертикальная сосредоточенная сила, приложенная в точке А балки, то соответствующим этой силе обобщенным перемещением (о.п.) является перемещение по направлению этой силы, то есть прогиб в точке А (рис. 4.17, а), так как именно на таком перемещении сила F совершает работу. Если обобщенной силой является сосредоточенная пара сил, приложенная в точке В, то обобщенным перемещением, соответствующим этой обобщенной силе, будет угол поворота в сечении В (рис. 4.17, б).
Запишем приближенную формулу Максвелла – Мора, которая используется для определения перемещений в изгибаемых плоских стержневых системах и не учитывает влияния на перемещения продольной и поперечной сил:
. (4.21)
В этой формуле – искомое обобщенное перемещение (это может быть и прогиб, и угол поворота любого сечения);М – изгибающий момент от заданной нагрузки; Мi – изгибающий момент, вызванный единичной обобщенной силой, соответствующей искомому перемещению; EI – жесткость стержня при изгибе (произведение модуля упругости на момент инерции). Интегрирование в формуле Максвелла – Мора ведется по длинам всех стержней конструкции (по длинам всех участков балки).
Таким образом, чтобы воспользоваться формулой Максвелла – Мора, надо:
- определить изгибающий момент на каждом участке от заданной нагрузки;
- освободить конструкцию от заданной нагрузки и загрузить ее единичной обобщенной силой, соответствующей искомому перемещению, то есть:
- если мы хотим определить вертикальное перемещение какой-то точки, то в этой точке следует приложить сосредоточенную силу, положить ее равной единице и найти изгибающий момент, вызванный действием только этой силы;
- если требуется найти угол поворота какого-то сечения, то в этом сечении надо приложить сосредоточенную пару, равную единице, и найти изгибающий момент от этой пары;
- подставить произведение изгибающих моментов от нагрузки и от единичной обобщенной силы в интеграл (4.21) и проинтегрировать по всей длине конструкции.
Введем правило знаков в методе Максвелла – Мора: полученный по формуле Максвелла – Мора положительный знак перемещения показывает, что искомое перемещение происходит по направлению, совпадающему с принятым направлением единичной обобщенной силы, отрицательный знак перемещения говорит о том, что точки оси перемещаются (сечения поворачиваются) в сторону, противоположную направлению единичной обобщенной силы. Очень распространенным способом интегрирования формулы Максвелла – Мора является способ графического интегрирования, называемый правилом Верещагина. Для того, чтобы воспользоваться правилом Верещагина, надо построить графики функций М и 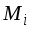

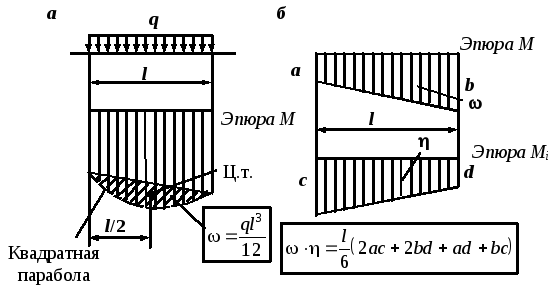
- Разбиваем эпюру М на простые фигуры, для которых известно положение центра тяжести (прямоугольники, треугольники и т. п.) 8 .
- Находим площади этих фигур
. При определении площадей учитываем знаки ординат.
- Под центрами тяжести этих фигур находим ординаты
на эпюре
(с учетом знаков).
- Искомый интеграл будет равен (при постоянной жесткости балки
) сумме произведений площадей
на соответствующие им ординаты под центрами тяжести
, то есть






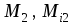


Источник
16 Формула мора порядок определения перемещений от внеш сил.
Примем, что на конструкцию действует статическая внешняя нагрузка, т.е. нагрузка, которая возрастает от нуля до своего предельного значения с такой скоростью, что возникающими инерционными силами можно пренебречь.
При малых деформациях, когда напряжения не превышают предела пропорциональности, применим принцип независимости действия сил.
Определим работу статической внешней нагрузки (P или m) приложенной к упругой системе, материал которой удовлетворяет закону Гука.
Перемещение некоторой точки от силы Р (рис. 8.1) будет:
,
где – коэффициент пропорциональности, его величина зависит геометрии сооружения, вида сечения и материала.
Поворот некоторого сечения от сосредоточенного момента m будет
.
В дальнейшем все рассуждения проведем на примере действия сосредоточенной силы Р и обобщим на другие случаи нагружения.
Увеличим силу Р на dP, что вызовет приращение перемещения d. Найдем величину элементарной работы внешней силы на перемещении d:
d
Найдем выражение для определения работы при изменении внешней силы от нуля до конечной величины:
.
Мы получили теорему Клапейрона:
Работа внешней силы при статическом ее приложении на сооружение равна половине произведения ее значения на величину соответствующего ей перемещения.
Легко обобщить полученный результат на случай, когда к сооружению приложена система статических внешних сил:
Определение перемещений. Интеграл Мора
Пусть требуется определить перемещение точки к от действия статически приложенной внешней нагрузки – Dкр (рис. 8.8 а).
Р ассмотрим вспомогательное состояние, когда к упругой системе в точке к приложена единичная сила Р2 = 1 (рис. 8.8 б).
Найдем работу силы Р2 = 1 второго состояния на перемещении Dкр, вызванном силами первого, действительного состояния А21:
Запишем выражение для определения :
, где Np, Qp, Mp – внутренние усилия от заданной внешней нагрузки;
– внутренние усилия, возникающие от единичной силы P2 = 1.
Получили формулу для определения перемещений – формулу Мора или полный интеграл Мора.
Для определения перемещений с помощью формулы Мора необходимо:
Определить выражения для внутренних усилий Np, Qp, Mp как функции координаты х произвольного сечения для всех участков стержневой системы от действия заданной нагрузки.
Приложить по направлению искомого перемещения соответствующую ему единичную нагрузку (единичную силу, если определяется линейное перемещение; сосредоточенный единичный момент, если определяется угловое перемещение).
Определить выражения для внутренних усилий как функции координаты х произвольного сечения для всех участков стержневой системы от действия единичной нагрузки.
Найденные выражения внутренних усилий в первом и втором состоянии подставляют в интеграл Мора и интегрируют по участкам в пределах всей стержневой системы.
17 Яастный случаи применения интегр мора для балок,рам,ферм и арок.
О ценка влияния поперечной силы Q на перемещения стержневой системы. В общем случае эпюра М от заданной нагрузки криволинейна (рис. 8.9 а). Ее с любой, наперед заданной точностью можно представить отрезками ломанной прямой (рис. 8.9 б).
Эпюра всегда линейна (рис. 8.9 в) и для простоты рассуждений представим, что треугольная.
Итак, , тогда поперечная сила
Так как 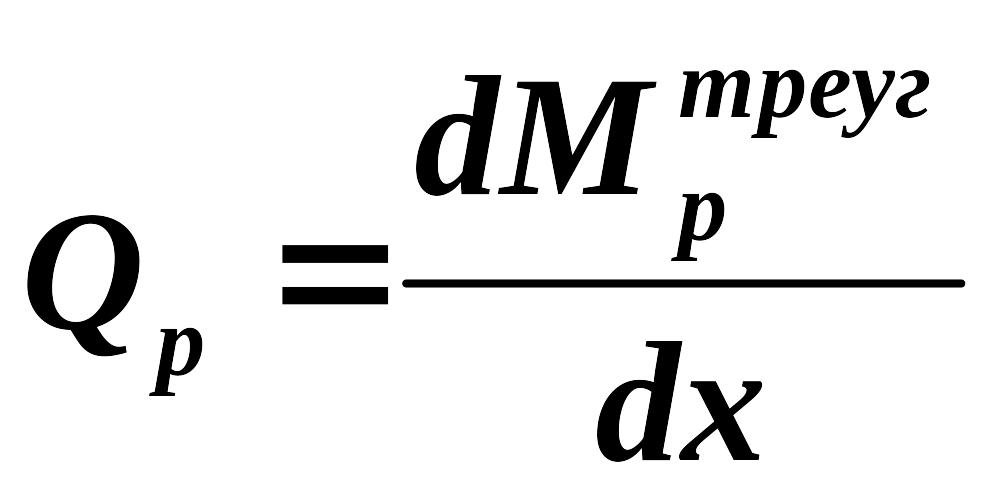
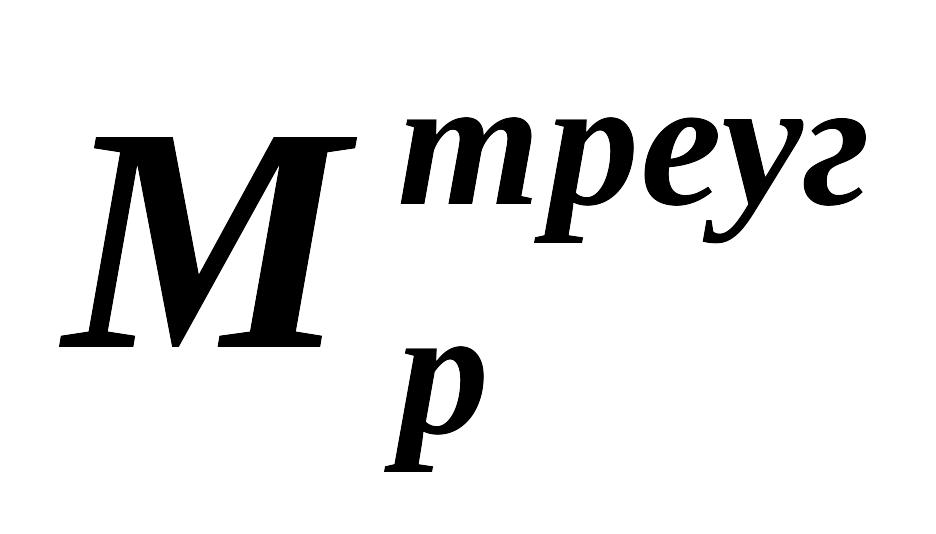
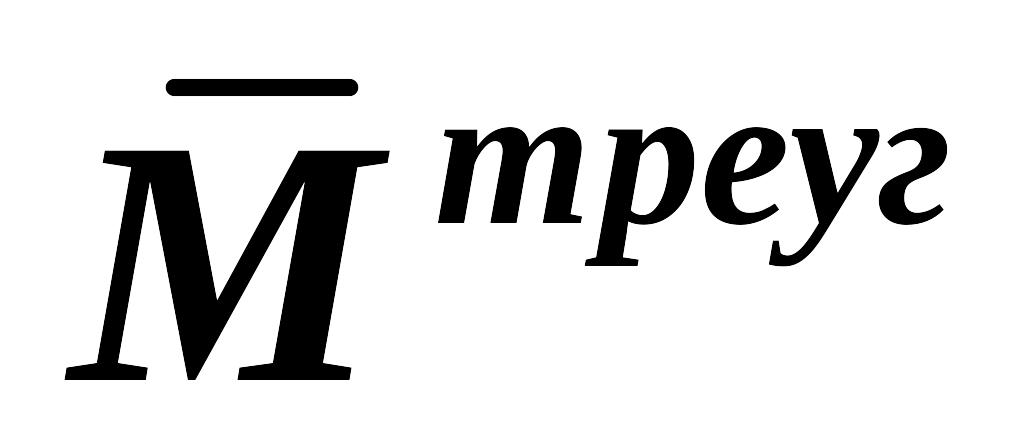
О чевидно, что 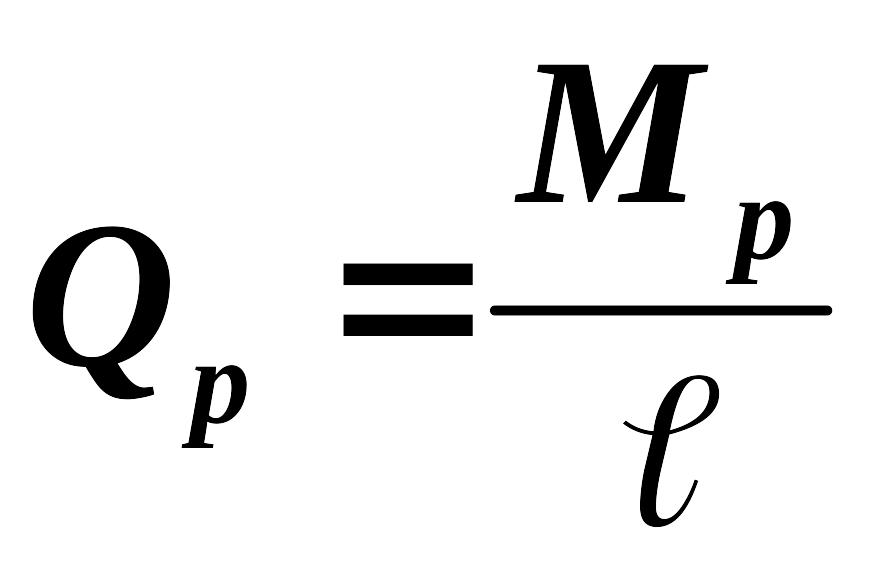
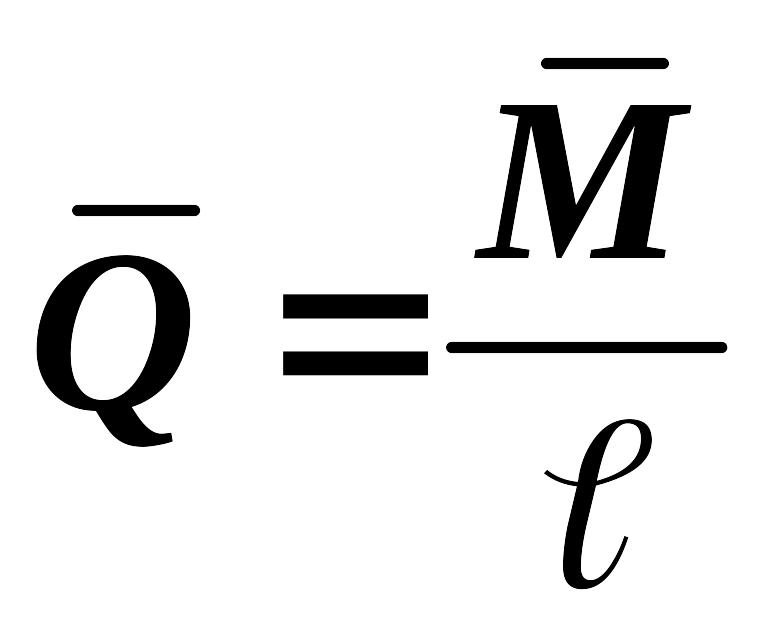

Найдем перемещение с учетом влияния изгибающих моментов и поперечных сил:
;
(применил способ Верещагина в первом и втором случаях, проделайте подробно самостоятельно);
– модуль упругости второго рода (модуль сдвига);
– момент инерции поперечного сечения стержня (предполагаем, что сечение стержня прямоугольное и b – ширина сечения, h – высота);
– площадь сечения стержня.
Найдем (проделайте самостоятельно).
Выражение для коэффициента ранее было получено:
,
где – статический момент отсеченной части поперечного сечения.
.
Для = 0,25 рассмотрим несколько случаев:
1. , т.е. влияние поперечных сил на перемещение составляет 3%.
2. , влияние поперечных сил уменьшается с увеличением длины стержня.
Так как в качестве объекта исследований принята стержневая система, в которой отдельные стержни всегда подчиняются принятому условию , то можно считать, что доказана возможность пренебречь влиянием поперечных сил.
Влияние нормальных сил N не будет превышать влияние поперечных сил на перемещения. Это следует из того, что одним из способов нахождения нормальных сил в рамах являются условия равновесия узлов, вырезанных в эпюре Q, т.е. N не превышают Q.
Определение перемещений в балках и рамах. Если рассматриваются стержневые системы, преимущественно работающие на изгиб, составленные из длинных и невысоких в сечении стержней, т.е. , то перемещения в таких конструкциях определим по формуле:
.
Фермы. В стержнях фермы возникают только нормальные усилия, поэтому
.
Арки. В арках при определении перемещений чаще приходится учитывать все внутренние факторы и только когда ось арки близка к рациональной, то достаточно учесть нормальные усилия.
Источник

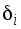
 . При определении площадей учитываем знаки ординат.
. При определении площадей учитываем знаки ординат. на эпюре
на эпюре 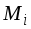 (с учетом знаков).
(с учетом знаков). ) сумме произведений площадей
) сумме произведений площадей на соответствующие им ординаты под центрами тяжести
на соответствующие им ординаты под центрами тяжести , то есть
, то есть