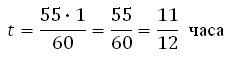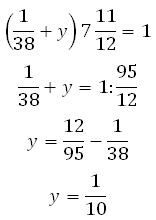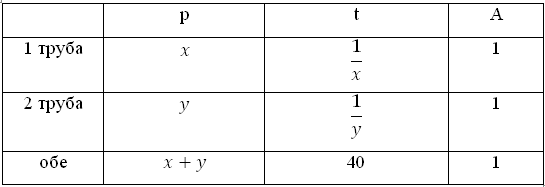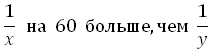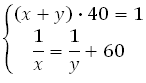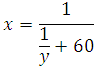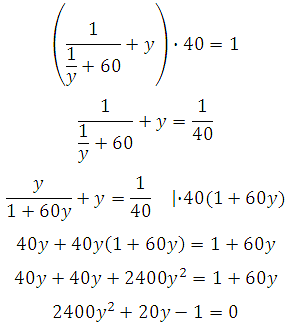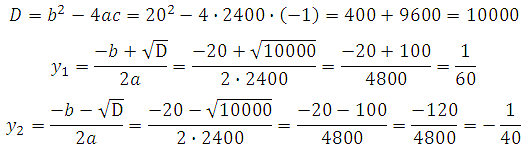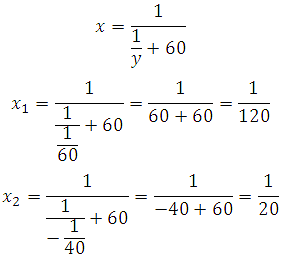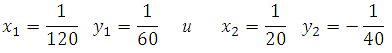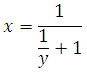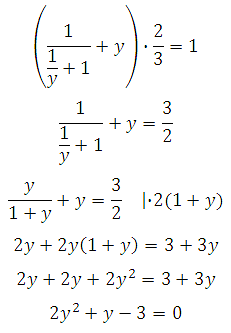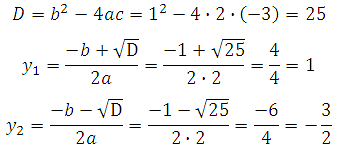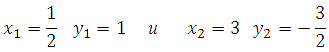Две трубы наполняют бассейн за 3 часа определи за сколько часов наполняет бассейн первая труба

Две трубы наполняют бассейн за 3 часа определи за сколько часов наполняет бассейн первая труба

Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

Пусть объем бассейна равен 1. Обозначим и — скорости наполнения бассейна первой и второй трубой, соответственно. Две трубы наполняют бассейн за 3 часа 36 минут:

По условию задачи одна первая труба наполняет бассейн за 6 часов, то есть Таким образом,

Тем самым, вторая труба за час наполняет 1/9 бассейна, значит, вторая труба наполняет этот бассейн за 9 часов.

Приведем другое решение.

Первая труба за час наполняет 1/6 бассейна, значит, за 3 ч 36 мин = 3,6 часа она заполнит 0,6 бассейна. Следовательно, вторая труба за 3,6 часа заполнит 0,4 бассейна. Поэтому весь бассейн она заполнит за время 3,6:0,4 = 9 часов.

Источник

Две трубы наполняют бассейн

Для вас ещё пара задач на работу. Здесь речь идет о наполнении резервуаров водой, ничего нового. Совместная работа.

Две трубы наполняют бассейн за 7 часа 55 минут, а одна первая труба наполняет бассейн за 38 часов. За сколько часов наполняет бассейн одна вторая труба?

Не забываем перевести минуты в часы. Кроме того, в этой задаче составим таблицу. Производительность первой трубы равна за 1/38 бассейна в час. Производительность второй трубы обозначим y.

Переведём минуты в часы.

Понятно, что 55 минут составляют 55/60 часа.

Можно составить пропорцию:

60 минута ––– 1 час

55 минут ––– t часов

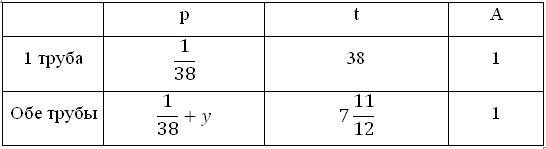
Заполним таблицу для первой трубы и двух труб работающих одновременно. Помним, что при совместной работе производительности складывают:

Можем записать уравнение:

Получили производительность второй трубы 1/10 (бассейна в час). Значит, весь бассейн она заполнит за 10 часов.

Первая труба наполняет резервуар на 60 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 40 минут. За сколько минут наполняет этот резервуар одна вторая труба?

Примем производительность первой трубы за х (резервуара в минуту), второй трубы у.

Составим таблицу, для первой и второй трубы заполним графу «время».

Первая труба будет заполнять резервуар за 1/х минут, вторая за 1/у минут.

Первая труба наполняет резервуар на 60 минут дольше, чем вторая, то есть времени затрачивается больше

Можем записать два уравнения и решить систему:

Выразим из второго уравнения х:

Подставим в первое уравнение и решим:

Решаем квадратное уравнение:

Подставим найденные значения у в уравнение:

Система имеет два решения:

Понятно, что производительность не может быть отрицательной. Решением является первая пара. Таким образом, первая труба заполнит 1/120 резервуара в минуту, а вторая 1/60 резервуара в минуту.

Следовательно весь резервуар второй трубой будет заполнен за 60 минут.

Можно минуты перевести в часы, тогда будем решать систему:

Выразим из второго х:

Подставим в первое уравнение и решим:

Решаем квадратное уравнение:

Подставим найденные значения у в уравнение:

Система имеет два решения:

Решением является первая пара. Первая труба заполнит ½ резервуара в час, а вторая 1 резервуар в час. То есть вторая труба наполнит его за 60 минут.

*Второй подход немного упрощает процесс вычисления, поэтому смело используйте если это вам будет удобно.

Источник

Две трубы наполняют бассейн за 3 часа определи за сколько часов наполняет бассейн первая труба

Две трубы наполняют бассейн за 18 часов 40 минут, а одна первая труба наполняет бассейн за 40 часов. За сколько часов наполняет бассейн одна вторая труба?

Это задание ещё не решено, приводим решение прототипа.

Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

Пусть объем бассейна равен 1. Обозначим и — скорости наполнения бассейна первой и второй трубой, соответственно. Две трубы наполняют бассейн за 3 часа 36 минут:

По условию задачи одна первая труба наполняет бассейн за 6 часов, то есть Таким образом,

Тем самым, вторая труба за час наполняет 1/9 бассейна, значит, вторая труба наполняет этот бассейн за 9 часов.

Приведем другое решение.

Первая труба за час наполняет 1/6 бассейна, значит, за 3 ч 36 мин = 3,6 часа она заполнит 0,6 бассейна. Следовательно, вторая труба за 3,6 часа заполнит 0,4 бассейна. Поэтому весь бассейн она заполнит за время 3,6:0,4 = 9 часов.

Источник