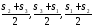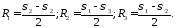Девиатор напряжений по кругам мора

11.10. Круги напряжений Мора

Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:

Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):

Координаты центра окружности , радиус .

Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:

Минимальное значение возникает на площадке при и равно:

Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).

Их уравнения в параметрической форме имеют вид:

откуда следует, что наибольшее касательные напряжения в этих случаях:

также равны радиусам соответствующих кругов Мора.

носят название главных касательных напряжений. Они удовлетворяют тождеству

Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:

Следовательно, определяется радиусом большого круга Мора. Величину

называют параметром вида напряжённого состояния Лоде. При наложе-

нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.

Таким образом, параметр Лоде характеризует вид напряжённого состояния.

Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):

Поступая так же, как и в случае двухосного растяжения сводим пара-

метрические уравнения окружности (11.63) к каноническому виду

В (11.64) мы имеем более сложное выражение радиуса окружности:

При уравнение (11.64) сводится к (11.60) как частному случаю.

При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами

Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-

нить правило знаков для и других напряжений, указанных на

рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-

положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-

ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-

льно противоположная Д, даёт напряжения для площадки, состав-

ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-

лом с осью х. Точка Д даёт максимальное касательное напряже-

ние, равное радиусу круга Мора:

Одной из важных задач использования круга Мора является определе-

ние главных нормальных напряжений и . Этим напряжениям отве-

чают точки Р₁ и Р₂ круга. Из рис. 11.26 следует, что угол между направле-

ниями на точки А и Р₁ равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р₂ – удвоенный угол , определяющий второе главное направление. Имеет место соотношение

которое совпадает с формулой (11.36).

Из изложенного следует, что круг Мора можно использовать в качес-

тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-

Источник

3. Разложение тензора напряжений

3.1. Запись тензора напряжений, заданного компонентами в главных площадках σ1, σ2, σ3. Вычисление гидростатического давления.

Тензор напряжений, заданный компонентами в главных площадках σ_1, σ_2, σ₃ запишется в виде

Подставив значения главных напряжений, получим:

(МПа)

3.2.Гидростатическое давление вычисляется по формуле:

(29)

Подставив значения главных напряжений, получим:

(МПа)

Разложение тензора напряжений, заданного компонентами в произвольно ориентированной площадке и в главных осях на шаровой тензор и девиатор напряжений.

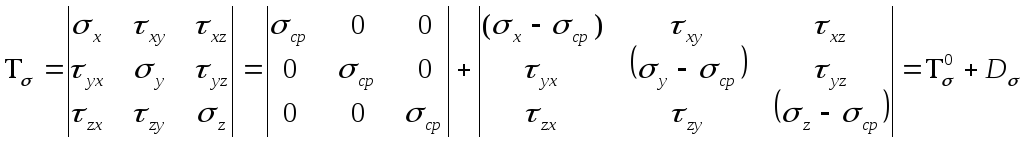
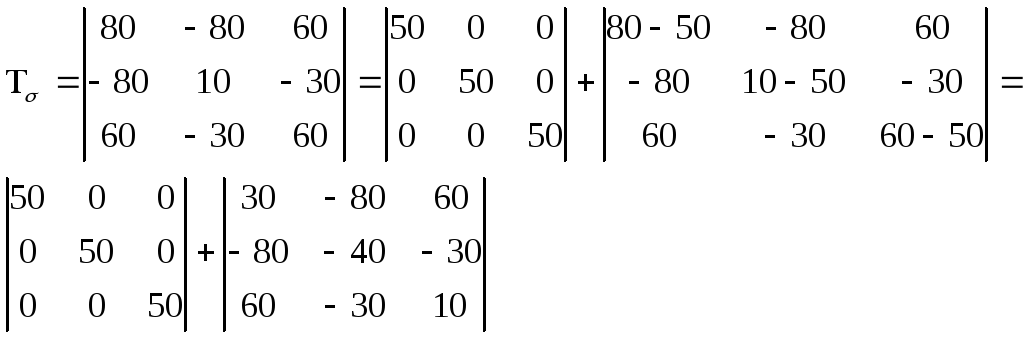
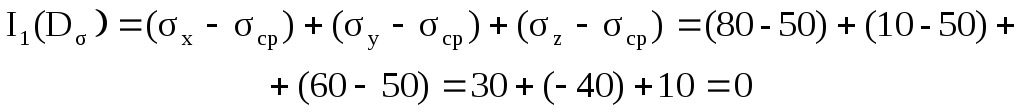
Тензор напряжений T_σ можно представить в виде двух слагаемых , (30) где — среднее напряжение; T_σ° — шаровый тензор напряжений; D_σ – девиатор напряжений. Шаровый тензор определяет напряженное состояние всесторон­него растяжения или сжатия, которое вызывает лишь чисто упругое изменение объёма тела без изменения его формы. Девиатор напряжений определяет напряжённое состояние, вызы­вающее пластическое формоизменение твёрдого тела без изменения его объёма, Особенностью девиатора является равенство нулю его первого инварианта I₁(D_σ). Разложение тензора напряжений, заданного компонентами в произвольно ориентированной площадке на шаровой тензор и девиатор напряжений. (МПа) Покажем, что первый инвариант девиатора напряжений равен нулю. Разложение тензора напряжений, заданного компонентами в главных осях на шаровой тензор и девиатор напряжений. Покажем, что первый инвариант девиатора напряжений равен нулю. Масштаб: в мм МПа = + = + Рисунок 2 — Разложение тензора напряжений, заданного компонентами в произвольно ориентированной площадке на шаровой тензор и девиатор напряжений. Масштаб: в мм МПа = + = + Рисунок 3 — Разложение тензора напряжений, заданного компонентами в главных осях на шаровой тензор и девиатор напряжений.

4. Вычисление главных касательных напряжений, интенсивности напряжений для главных и произвольно ориентированных площадок и значения нормального и касательного октаэдрических напряжений.

4.1. Вычисление главных касательных напряжений.

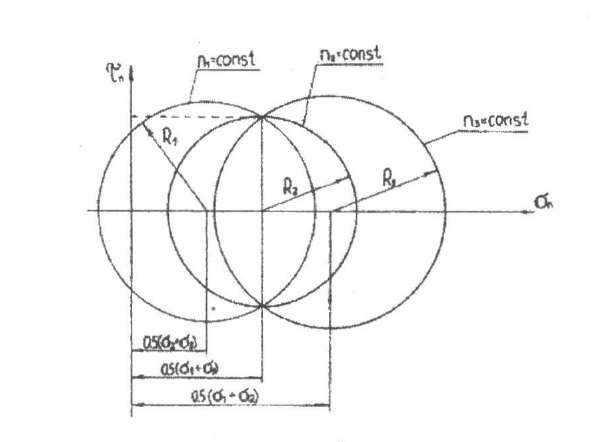
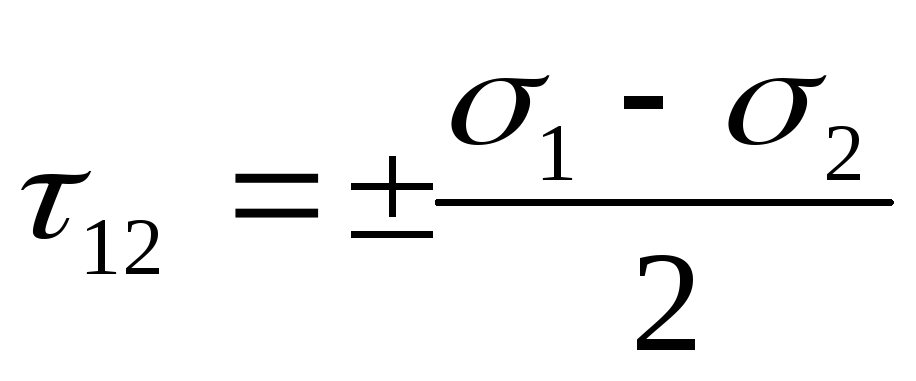
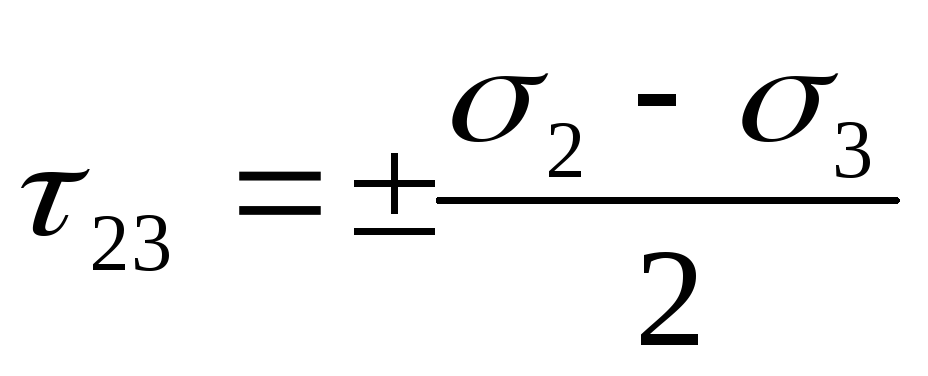
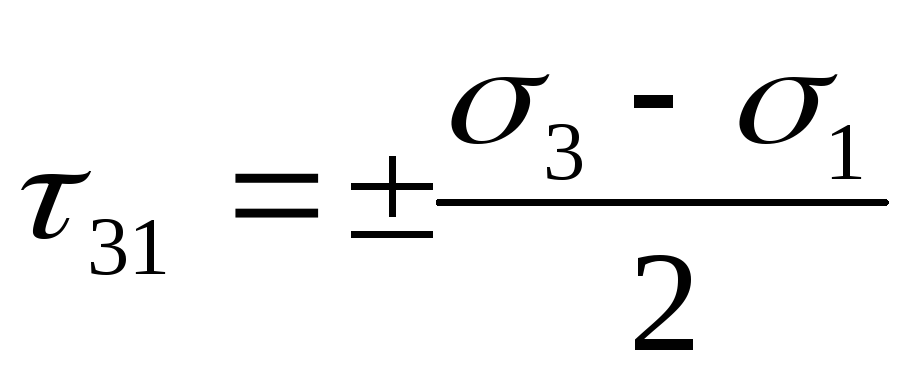
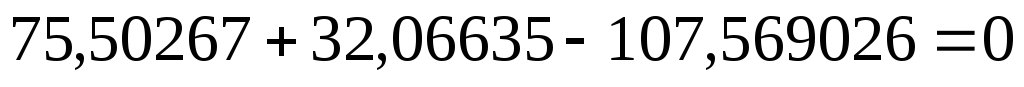
Главные касательные напряжения действуют в площадках, наклоненных под углом 45° к главным осям, вдоль которых направлены главные нормальные напряжения. Определяются они как полуразность двух соответствующих главных нормальных напряжений _{(31) (32) (33)} Подставив численные значения получим: (МПа) (МПа) (МПа) Выполним проверку из условия, что сумма главных касательных напряжений равна нулю: 0=0

Источник

1.11. Диаграмма напряжений Мора

Диаграммы напряжений Мора дают наглядное графическое представление о совокупности векторов нормальных и касательных напряжений на наклонных площадках, построенных в системе главных осей. При построении диаграммы нормальные напряжения будем откладывать на оси абсцисс, а касательные по оси ординат. Нормальные напряжения в главных осях:

(16)

(17)

Направляющие косинусы связаны соотношением:

(18)

Получаем линейную относительно n₁ 2 систему всех уравнений (16)-(18). Умножим обе части уравнения (16) на σ₂+σ₃:

(19)

а уравнение (18) умножим на σ₂σ₃:

(20)

Из уравнения (17) почленно вычтем уравнение (19) и, прибавив почленно уравнение (20), получим:

Прибавляя к обеим частям полученного уравненияпосле преобразования получим:

(21)

Записанное уравнение (21) определяет окружности вида (x-x0)2+y2=R2. Их центры расположены на оси абсцисс и отстоят от начала координат на расстоянии (рис. 22). В правой части уравнения (21) n1, n2, n3 — это изменяемые параметры, поэтому каждое из уравнений (21) — это уравнение концентрических окружностей с радиусами

Первое уравнение системы (21) определяет в виде окружностей геометрическое место точек σ_n и τ_n для заданного значения n₁. То же самое справедливо и для двух других уравнений системы. Для заданных значений направляющих косинусов n₁, n₂, n₃ и главных нормальных напряжений σ₁, σ₂, σ₃ величины σ_n и τ_n определяются точкой К на пересечении трех окружностей радиусами R_1, R₂, R₃, при n₁=n₂=n₃=0 радиусы окружностей равны:

Как видно из первого и третьего уравнения системы (21), при увеличении n1 и n2 радиусы соответствующих окружностей увеличиваются. Это означает, что возможные пары значений σn и τn находятся или на окружностях радиуса R1 или R3, или вне их, но не могут располагаться внутри. Если увеличивать n2 (второе уравнение системы (20)), то R2 уменьшается и пары σn и τn находятся внутри окружности R2. Таким образом, заштрихованная область — это область значений σn и τn на произвольных наклонных площадках (рис. 23).

Из формулы (21) видно, что максимальные касательные напряжения численно равны радиусам кругов. При наложении на тело всестороннего равномерного давления радиусы окружностей не меняются, и все построения смещаются относительно горизонтальной оси σ_n.

Шаровой тензор напряжений отображается на диаграмме Мора окружностью нулевого радиуса (т. е. точкой), расположенной на расстоянии σ_ср от начала координат.

1.12. Выводы

В этой главе рассмотрены вопросы теории напряжении. Напряженное состояние в исследуемой точке твердого деформируемого тела характеризуется девятью компонентами напряжений σ_ij, заданными в произвольной системе координат, которые образуют тензор напряжений Т_σ. Из девяти компонентов напряжений независимых только шесть, так как по закону парности составляющие касательных напряжений попарно между собою равны, т. е. тензор напряжений является симметричным тензором. Имея компоненты тензора напряжений на трех взаимно перпендикулярных площадках по соотношениям Коши, можно вычислить составляющие напряжений по любым наклонным площадкам. Одновременно соотношения Коши можно рассматривать как условия на поверхности тела, если наклонная площадка совмещена с поверхностью тела.

Разложение тензора напряжений на девиатор и шаровой тензор обусловлено тем обстоятельством, что материалы имеют различные механические свойства по отношению к равномерному всестороннему растяжению (или сжатию) и к касательным напряжениям. Шаровой тензор напряжений характеризует объемную деформацию в точке, а девиатор напряжений — формоизменение в окрестности точки.

При анализе напряженного состояния точки используются следующие характерные площадки, проходящие через нее: 58

три главные площадки, на которых действуют главные нормальные напряжения, а касательные отсутствуют;

шесть площадок, по которым действуют главные касательные напряжения; площадки, в которых возникают главные касательные напряжения, делят пополам прямые углы между главными площадками;

четыре площадки, равнонаклонные к главным осям, на которых действуют одинаковые по величине октаэдрические напряжения.

Геометрическим образом объемного напряженного состояния в точке деформируемого тела служит эллипсоид напряжений. Полуосями его являются главные нормальные напряжения σ₁, σ₂ и σ₃. Поверхность эллипсоида напряжений представляет собой геометрическое место концов векторов полных напряжений в различных площадках, прохо­дящих через рассматриваемую точку. Из эллипсоида напряжений следует экстремальность главных напряжений, т. е. одно из главных напряжений является наибольшим, а другое наименьшим из всех нормальных напряжений в площадках, проходящих через рассматриваемую точку.

Диаграмма напряжений Мора представляет собой плоский геометрический образ напряженного состояния. Она состоит из трех полуокружностей, диаметрами которых являются разности главных напряжений. Координаты точек, лежащих в заштрихованной области между полуокружностями, представляют собой нормальные и касательные напряжения в произвольно ориентированных площадках.

Показатель вида напряженного состояния Лоде-Надаи характеризует с точностью до равноосного растяжения (сжатия) вид напряженного состояния.

Источник