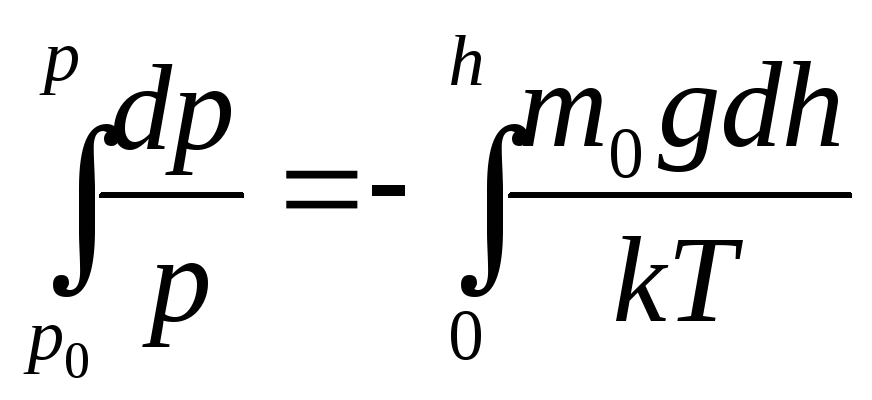Давление газа над уровнем моря

В чем особенности статистического и термодинамического подходов к изучению газовых систем?

Что такое броуновское движение частиц вещества малых размеров, чем оно вызвано и о чем свидетельствует?

Бро́уновское движе́ние — беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа. Было открыто в 1827 году Робертом Броуном. Броуновское движение никогда не прекращается. Оно связано с тепловым движением, но не следует смешивать эти понятия. Броуновское движение является следствием и свидетельством существования теплового движения. Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют), более мелкие частицы (менее 3 мкм) двигаются поступательно по весьма сложным траекториям или вращаются.

1. Как проводился опыт Штерна и что он показал?

для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. Далее пропускался ток и серебро плавилось В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.

1. О чем говорит закон Максвелла о распределении молекул идеального газа по скоростям?

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что внешние поля на газ не действуют.

1. Как соотносятся друг с другом наиболее вероятная, средняя и среднеквадратичная скорости движения молекул газа?

1. Как выглядит барометрическая формула и что она означает?

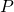
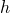
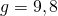
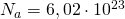
Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести — Давление газа (атмосферное) — Давление газа над уровнем моря — Высота над уровнем моря — Плотность газа — Ускорение свободного падения — Постоянная Больцмана — Температура — Масса одной молекулы — Универсальная газовая постоянная — Молярная масса — Количество вещества — Число Авогадро

1. Что такое длина свободного пробега молекул? От чего она зависит? Каким образом?

Длина свободного пробега молекулы — среднее расстояние, которое частица пролетает за время свободного пробега от одного столкновения до следующего. Средняя длина свободного пробега молекулы Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега l. 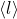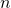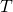Величина l является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры Если нам нужно выразить формулу через давление и температуру, то производим маленькую замену в 1 части формулы: p=nkT n= kT/p Заменяем количество вещества на полученную нами формулу, и у нас получается: — Длина свободного пробега молекулы — Эффективный диаметр молекулы — Концентрация молекул — Давление — Постоянная Больцмана — Температура, при которой находится газ

Источник

Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести

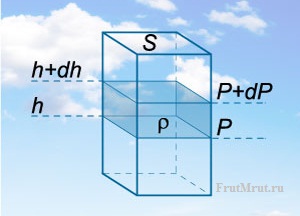
Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как:

Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP:

Знак минус необходим для того, что с увеличением высоты давление уменьшается

Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона

Из этого уравнения выражаем давление

А теперь можно и плотность газа

Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем:

Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:

Проинтегрировав, у нас полечилась вот такое уравнение:

И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.

В Формуле мы использовали:

— Давление газа (атмосферное)

— Давление газа над уровнем моря

— Ускорение свободного падения

— Универсальная газовая постоянная

Концентрация молекул n — число молекул в единице объема.

Другие формулы, где встречается концентрация молекул:

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

n = n ₀exp(- mgh / kT)

где n — концентрация молекул на высоте h, n ₀ — концентрация молекул на начальном уровне h = 0, m — масса частиц, g — ускорение свободного падения, k — постоянная Больцмана, T — температура.

Если высота сосуда много меньше чем kT / mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. Принимая во внимание, что P = nkT, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты:

P = P ₀exp(- mgh / kT)

Воспользуйтесь поиском по сайту:

studopedia.org — Студопедия.Орг — 2014-2023 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.01 с) .

Источник

Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести

Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как:

Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP:

Знак минус необходим для того, что с увеличением высоты давление уменьшается

Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона

Из этого уравнения выражаем давление

А теперь можно и плотность газа

Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем:

Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:

Проинтегрировав, у нас полечилась вот такое уравнение:

И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.

В Формуле мы использовали:

— Давление газа (атмосферное)

— Давление газа над уровнем моря

— Ускорение свободного падения

— Универсальная газовая постоянная

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Это важно знать:

Формирование и распределение прибыли предприятия Эффективность политики управления прибылью предприятия определяется результатами ее формирования и характером распределения.
Введение. Во введении курсовой работы описывается актуальность темы, цель, задачи, предмет и объект, методы исследования Во введении курсовой работы описывается актуальность темы, цель, задачи, предмет и объект, методы исследования.
Понятие деятельности в психологии Введение При осознании своего предмета психология не замыкается только на изучении психических процессов.
Основные, вспомогательные и обслуживающие подразделения предприятия. (47 вопрос) Производственный процесс состоит из частичных процессов, которые можно разделить на группы по следующим признакам.
Заполните таблицу в соответствии с теоретическим материалом Лабораторная работа № 1 Тема: устройства ПК Цель: изучение основных компонентов персонального компьютера и основных видов.

Источник

Идеальный газ в силовом поле. Барометрическая формула

Найдем закон изменения давления газа в зависимости от высоты над уровнем моря, полагая, что газ идеальный, темпера­тура его постоянна и не изменяется с высотой, ускорение свобод­ного падения не зависит от высоты. Последние два предположе­ния справедливы при относительно небольших изменениях высоты.Выделим мысленно, на высотеНнад уровнем моря ци­линдрический слой, высота которогоdh,а основание равноS(рис. 8).где=m₀gnSh— сила притяжения молекул объемаShк Земле;=pS— сила давле­ния на высотеh;= (р +dp)S— сила давления на высотеh+dh.Все силы направлены по одной прямой, поэтомуF_T+F₂–F₁= 0.сокращая наSи учитывая, что, получимРазделяя переменные и принимая во внимание, что =const.(1.2)— Барометрическая формула(1.2);т.к. , тоНа основе барометрической формулы разработаны приборы- алтиметры- приборы для определения высоты.

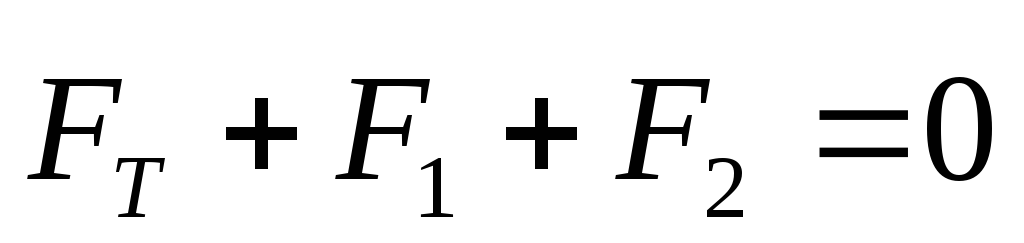
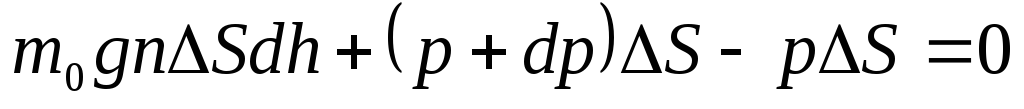
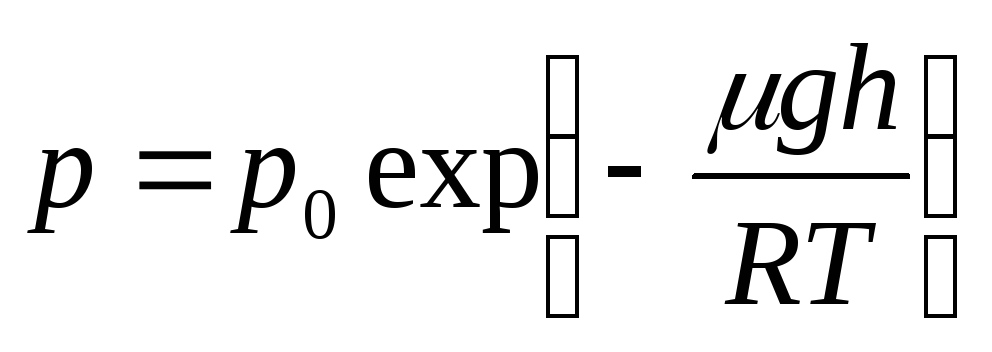
Закон Больцмана

Пользуясь барометрической формулойУчитывая, чтор = nkT,р₀= n₀kT,гдепип₀—концентрации молекул соответственно на высоте h иh₀(1.2)Полученное распределение Больцмана справедливо для по­ля тяготения. Однако оно справедливо и для газа, находящегося в любом дру­гом потенциальном поле. При этом величинаm₀ghзаменяется наW_П— потенциальную энергию молекулы в произвольном силовом поле.(1.2)ЕслиkTW_п,имеет место почти равномерное распределение частиц по энергиям (распределение Максвела).ПриkTW_п,nn₀, т.е. имеет место резкое изменение концентрации молекул в силовом поле: число молекул с небольшими энергиями (на низких энергетических уровнях) значительно превышает число молекул на более высоких энергетических уровнях.Распределение Больцмана, описываемое функцией (1.37) называется нормальным распределением. В 1905 г. Эйнштейн предсказал существование систем с инверсной заселенностью энергетических уровней. В 1960 г впервые такое распределение использовано практически- в лазерах.Для характеристики инверсных систем в физике ввели понятие Т0.Распределение Максвелла-Больцмана, описывающие распределение молекул по скоростям в силовом поле.(1.2)

Источник