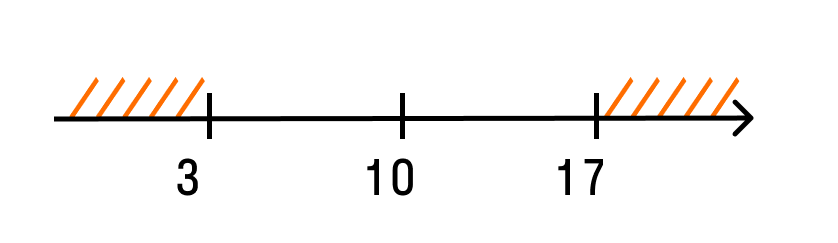Что такое мор математика

МОР — методы оптимальных решений в экономике

Методы оптимальных решений – это совокупность приемов и способов, применение которые позволяет найти в заданных условиях наилучший (т.е. оптимальный) результат.

Сущность методов оптимальных решений в экономике

Главная проблема экономической науки, которая предопределило ее существование, заключается в ограниченности находящихся в распоряжении человечества ресурсов при том, что его потребности являются безграничными. В связи с этим экономика должна давать людям ответы на то, какой вариант экономических действий в заданных условиях является наилучшим (т.е. оптимальным). В данном случае одним из главных инструментов экономистов является система методов оптимальных решений (МОР).

Определение оптимального варианта решения конкретной экономической задачи может быть выражено в качестве процесса определения экстремума (т.е. максимума или минимума на заданном отрезке) целевой функции: W = f (a1, a2, …; b1, b2, …; x1, x2, …). В представленной целевой функции a1 и a2 являются заданными из вне (экзогенными) параметрами экономической задачи, b1 и b2 – управляемыми параметрами задачи (их значение может быть изменено исследователями), x1 и x2 – неизвестные параметры задачи.

Целевая функция является показателем успешности решения экономической задачи на нахождение оптимального (наилучшего) результата. Выбор данной целевой функции (т.е. показателя успешности) делается на основе принципа, который впервые был обоснован академиком А.Н. Колмогоровым еще в 1945 г. Этот принцип заключается в установлении строгого соответствия между целью, которая может быть достигнута в результате действий, и избранным показателем успешности.

Определение оптимального решения экономической задачи состоит из процессов поиска таких значений управляемых параметров (b), которые при заданных параметрах (a), целевая функция достигнет своего максимального значения.

Проблемы применения методов оптимальных решений в экономике

Применение методов оптимальных решений экономических задач обычно связано с наступлением ряда существенных проблем, трудностей, которые экономистам-исследователям приходится преодолевать. Основными из них на данный момент считаются следующие проблемы:

• необходимость перебора огромного числа (около нескольких десятков) управляемых параметров, что требует проведения кратно большего числа расчетных операций – из-за этого реальной является угроза невыполнения требуемых действий в заданные сроки (решение этой проблемы заключается в применении методов направленного перебора);
• при решении задачи требуется не только найти оптимальное (максимальное или минимальное) значение избранного показателя успешности, но и удовлетворять ряду дополнительных требований, например, ограничениям по времени решения задачи, по объемам доступных материальных средств и т.п.);
• присущее некоторым задачам производственного характера неполнота или отсутствие информации и необходимость принятия важных управленческих решений в условиях неопределенности (в этом случае обращаются к аппаратам статистики и теории игр);
• использование вычислительной техники зачастую приводит к результатам, которые значительным образом отличаются от результатов применения здравого смысла и соблюдения современных принципов научного исследования.

Алгоритм принятия оптимальных решений в экономике

Методы оптимальных решений позволяют проанализировать проблемную ситуацию, что является основным элементом всего процесса принятия управленческого решения. Проблемная ситуация подлежит всестороннему исследованию, что значительно повышает степень целесообразности и обоснованности принимаемого решения.

Для того, чтобы принимаемое решение оказалось оптимальным, необходимо по итогам анализа проблемной ситуации составить несколько вариантов решения, а затем сделать выбор между ними. Причем сама ситуация принятия оптимального управленческого решения состоит из следующих элементов:

• множество мотивирующих целей – разрабатывается и уясняется основная (главная) цель, в результате чего формируется система подцелей, достижение которых должно обеспечить принимаемое решение;
• множество допустимых стратегий, т.е. планов, которые могут быть выбраны лицами, принимающими решения на основании опыта и имеющейся информации, и реализована ими или другими ответственными перед ними лицами;
• множество состояний обстановки, среды — параметры состояний (речь идет про обстоятельства, которые могут произойти, не поддаются полному контролю со стороны лиц, принимающих решения, но оказывают влияние на ход принятия решения и на конечный результат);
• множество следствий (исходов) реализации множества соответствующих альтернативных стратегий при тех или иных обстоятельствах среды.

Методы оптимальных решений в условиях риска

Преимуществом большего числа методов оптимальных решений является возможность их эффективного (результативного) применения в условиях риска и неопределенности. А эти условия являются свойственными современным экономическим отношениям.

Риск – это объективное явление, которое обусловлено неоднозначностью событий будущего и связано с ущербом, потерей, упущенными возможностями. Методы оптимальных решений позволяют свести степень риска при принятии управленческого решения до минимального значения.

В условиях риска для определения оптимальных решений могут быть использованы критерии гарантированного результата, оптимизма, пессимизма и наименьшего вреда. Перечисленные критерии позволяют оценить все возможные альтернативные варианты управленческих решений и выбрать наилучший из них. В настоящее время указанные критерии в основном применяются комплексно, что позволяет как сохранить преимущества каждого из критериев, так и нивелировать их недостатки.

Источник

Теорема Мора

Теорема Мора — Маскерони сводит построения циркулем и линейкой к построениям одним циркулем. Точнее говоря, возможно провести одним только циркулем такие операции, для которых могла бы потребоваться линейка:

1. По данным точкам A, B, C, D найти точку пересечения прямых AB и CD.
2. По данной окружности S и двум точкам A и B найти точки пересечения прямой AB с окружностью S. Центр окружности считается заданным.

История

Результат был опубликован Георгом Мором в 1672 году [1] но доказательство было забыто до 1928. [2] [3] Теорема была независимо открыта Лоренцо Маскерони в 1797. [4]

См. также

Литература

Примечания

1. ↑ Georg Mohr, Euclides Danicus (Amsterdam: Jacob van Velsen, 1672).
2. ↑ Hjelmslev, J. (1928) «Om et af den danske matematiker Georg Mohr udgivet skrift Euclides Danicus, udkommet i Amsterdam i 1672» [Of a memoir Euclides Danicus published by the Danish mathematician Georg Mohr in 1672 in Amsterdam], Matematisk Tidsskrift B , pages 1-7.
3. ↑ Schogt, J. H. (1938) «Om Georg Mohr’s Euclides Danicus,» Matematisk Tidsskrift A , pages 34-36.
4. ↑ Lorenzo Mascheroni, La Geometria del Compasso (Pavia: Pietro Galeazzi, 1797).

Ссылки

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Теорема Мора» в других словарях:

• Теорема Мора — Маскерони — Теорема Мора Маскерони сводит построения циркулем и линейкой к построениям одним циркулем. Точнее говоря, возможно провести одним только циркулем операции, для которых могла бы потребоваться линейка: По данным точкам A, B, C, D найти точку… … Википедия
• Мор, Георг — Георг Мор дат. Jørgen Mohr Дата рождения: 1 апреля 1640(1640 04 01) Место рождения: Копенгаген, Дания … Википедия
• Маскерони — (итал. Mascheroni) фамилия итальянского происхождения Эрнесто Маскерони уругвайский футболист Лоренцо Маскерони итальянский математик. См. также Постоянная Эйлера Маскерони Теорема Мора Маскерони … Википедия
• УСТОЙЧИВОСТЬ ПО ПУАССОНУ — свойство точки ж (траектории f tx )динамич. системы f t (или см. [2]). заданной на топологич. пространстве S. состоящее в следующем: найдутся последовательности такие, что Иными словами, хявляется и предельной точкой траектории f tx. Понятие У.… … Математическая энциклопедия
• Построение с помощью циркуля и линейки — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности: Линейка не имеет делений и имеет сторону бесконечной … Википедия
• Построение циркулем и линейкой — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку… … Википедия
• Построения при помощи циркуля и линейки — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку… … Википедия
• Построения с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку пересечения двух построенных линий. С помощью… … Википедия
• Понедельник начинается в субботу — Понедельник начинается в субботу … Википедия

Источник

Модуль числа

Разберем сегодня, что значит модуль числа, как считать модуль и как обозначается модуль в математике. А также его свойства и, конечно же, примеры.

· Обновлено 21 октября 2022

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.

Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.

Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.

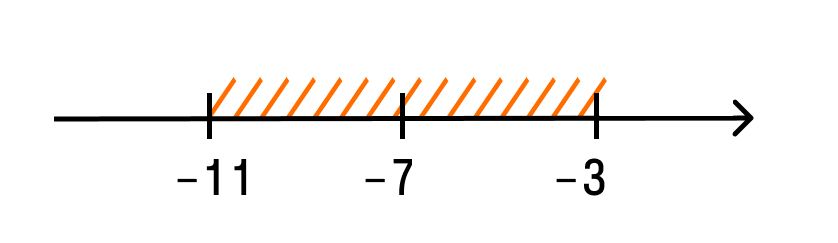
Решим неравенство: |a + 7| < 4.

Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:

Ответ в данном случае будет таким: (−11; −3).

Решим неравенство: |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.

График функции

График функции равен y = |х|.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.

По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .

Оно равно a при а > 0 и −а, при а < 0 , т. е. как раз |a|.

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Источник