Чему должна быть равна глубина бассейна с квадратным дном 256
Цитата: neytron40 написал 10 марта 2009 22:34
задача на применение производной.
определить размеры открытого бассейна объемом 256 см3 с квадратным дном у которого на его облицовку было израсходовано наименьшее кол-во плитки.
Мне кажется, решать надо так
Дно бассейна представляет собой квадрат. Пусть его сторона равна a. Пусть высота бассейна равна h. Необходимо определить a, h.
Так как было затрачено наименьшнн количество плитки, это означает, что площадь поверхности бассейна минимальна.
Площадь поверхности бассейна равна
S = (a^2) + 4ah.
Известно, что объем бассейна равен 256, то есть
(a^2)*h = 256
h = 256/(a^2)
S = (a^2) + 4*a*256/(a^2) =
= (a^2) + 1024/a
Необходимо найти такое a, при котором S минимальна.
S’ = 2a — 1024/(a^2)
S’ = 0
2a — 1024/(a^2) = 0
2a = 1024/(a^2)
(a^3) = 512
a = 8
h = 256/(a^2) = 256/64 = 4
Дно бассейна представляет собой квадрат, сторона которого равна 8 см. Высота бассейна равна 4 см.
| neytron40 |     спасибо огромное..эта последняя найти наименьшее и наибольшее значения функции z=f(x,y) в заданной области. z=x^2-2xy+2y^2+2x , -3 Всего сообщений: 35 | Присоединился: март 2009 | Отправлено: 11 марта 2009 20:54 | IP |
| grignata |  доброго времени суток, помогите найти производную от y=(lg(4x-3))^arccos(4x) и решить задачку Из бумажного круга вырезан сектор, а из оставшейся его части склеена коническая воронка. Какой угол должен иметь вырезанный сектор, чтобы объём воронки был наибольшим? спасибо |
| Всего сообщений: 30 | Присоединился: февраль 2009 | Отправлено: 12 марта 2009 10:22 | IP |
| Lipa1990 | Помогите доделать производные, 16.03 нужно уже сдать. Вообщем нужно найти произвоную 2го порядка от y=sin x/3 и y=(ln x)/Корень(x) 1го порядка от y=xln(x-1) Мои попытки:  — 1е  — 2е (как от этого найти 2ю производную, незнаю. (Сообщение отредактировал Lipa1990 14 марта 2009 15:08) |
| Всего сообщений: 14 | Присоединился: март 2009 | Отправлено: 14 марта 2009 15:02 | IP |
RKI  | y(x) = sin(x/3) y»(x) = (1/2)*(-3/2)*(x^(-5/2))*(2-lnx) + |
| Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 14 марта 2009 15:59 | IP |
| Lipa1990 | Спасибо Огромное за решение! Щас вот думаю, в 2м задании (lnx/sqrt(x)), нужно найти точки перегиба, для этого необходимо найти корни управнения. Что подставить чтоб уравнение = 0 ? + еще 1 вопросик в 1м задании нужно вычислить значение при указанном значении х: f(x)=sin x/3 f»(3) Подставляем в производную: f(3)=-(sin(3/3))/9 = . просто -sin/9 ? |
| Всего сообщений: 14 | Присоединился: март 2009 | Отправлено: 14 марта 2009 17:40 | IP |
| RKI |
y»(x) = 0 Необходимо анализировать меняет ли знак вторая производная при переходе через точку x = e^(8/3) и x=0 |
| Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 14 марта 2009 18:16 | IP |
| RKI |
+ еще 1 вопросик Источник Практическое применение производнойРассмотрим задачи, связанные с практическим применением производной. При их решении не дается готовой функции для исследования, а ее нужно составить самостоятельно по условию задачи. При этом сначала следует установить, какую величину выбрать за независимую переменную. В задачах, где выбор может быть сделан не единственным образом, следует остановиться на таком выборе, при котором исследуемая функция оказывается более простой. 610. Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.
612. Путь s , пройденный за время t материальной точкой, брошенной вертикально вверх с начальной скоростью vo , выражается формулой
613. Требуется вырыть силосную яму объемом 32 м 3 , имеющую квадратное дно, так чтобы на облицовку ее дна и стен пошло наименьшее количество материала. Каковы должны быть размеры ямы?
Найдем производную S по х:
614. Имеется квадратный лист жести, сторона которого
Найдем значение х, при котором функция примет наибольшее значение. Для этого сначала преобразуем функцию, а затем исследуем ее на экстремум:
Очевидно, что значение
т.е. при квадрата должна быть равна при а = 60см получим 615. Из круглого бревна радиуса R требуется вырезать прямоугольную балку максимальной прочности. Известно, что прочность балки прямо пропорциональна произведению се ширины
Находим производную и приравниваем ее нулю:
616. Оросительный канал имеет форму равнобочной трапеции,
Приравняем производную нулю и решим полученное уравнение:
617. Суточные расходы при плавании судна состоят из двух
функция при v = 0 имеет бесконечный разрыв, но нулевая скорость для нас не представляет интереса.
618. Разложить число а на два слагаемых так, чтобы их произведение было наибольшим. 619. Найти такое число, чтобы разность между этим числом и его квадратом была наибольшей. 620. Найти такое число, чтобы разность между этим числом 621. Окно имеет форму прямоугольника, завершенного полу 622. Тело движется по закону 623. Количество Q вещества, получающегося в процессе химической реакции, выражается формулой 624. Прилегающую к дому прямоугольную площадку нужно 625. Определить размеры открытого бассейна объемом 256 м 3 , имеющего квадратное дно, так чтобы на облицовку его стен и 626. Какой из равнобедренных треугольников с заданным 627. Найти отношение высоты к диаметру конуса, имеющего 628. Из всех цилиндров с площадью полной поверхности
Последнее изменение этой страницы: 2019-04-09; Просмотров: 784; Нарушение авторского права страницы Источник |
, где g — ускорение силы тяжести. Определить высоту наибольшего подъема точки.
. Вырезая по всем его углам равные квадраты и загибая оставшуюся часть, нужно изготовить коробку (без крышки). Каковы должны быть размеры вырезаемых квадратов, чтобы коробка имела наибольший объем?
не отвечает условию, так как в этом случае квадрат был бы разрезан на четыре равные части и никакой коробки не получилось бы. Поэтому исследуем функцию на экстремум в критической очке 
достигается максимум. Итак, сторона вырезаемого
. В данном конкретном случае
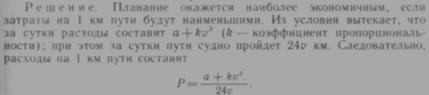
. Найти его максимальную скорость.
, где t — время. Найти максимальную скорость реакции.
найти тот, который имеет наибольший объем.