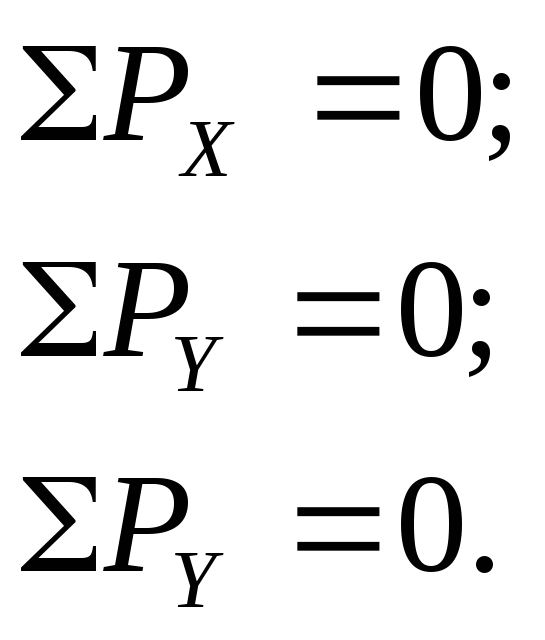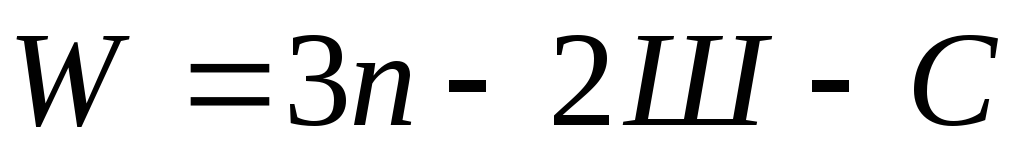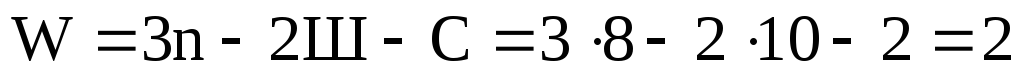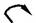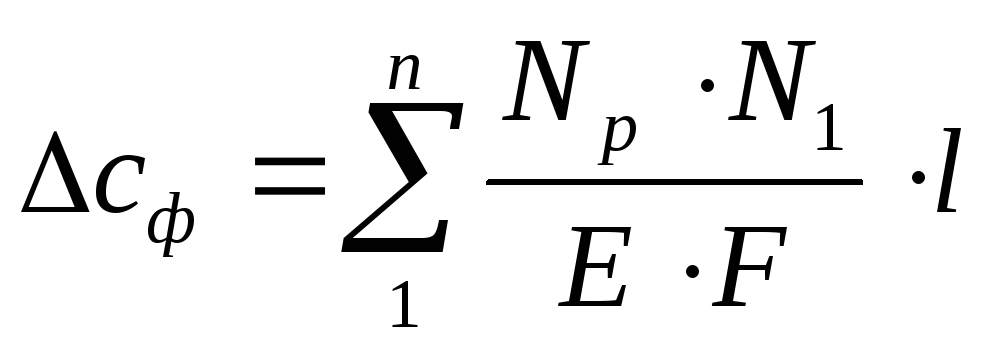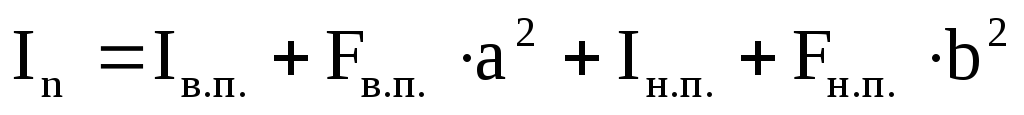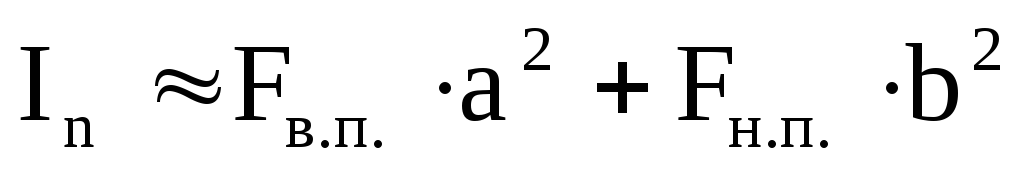Частные случаи формула мора

3 Расчетные схемы строительной механики

В строительной механике разработано несколько характерных расчетных схем, которые используются в расчетной практике, а именно:

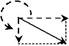
1 Балка – это стержень, преимущественно работающий на изгиб (рис. 1).

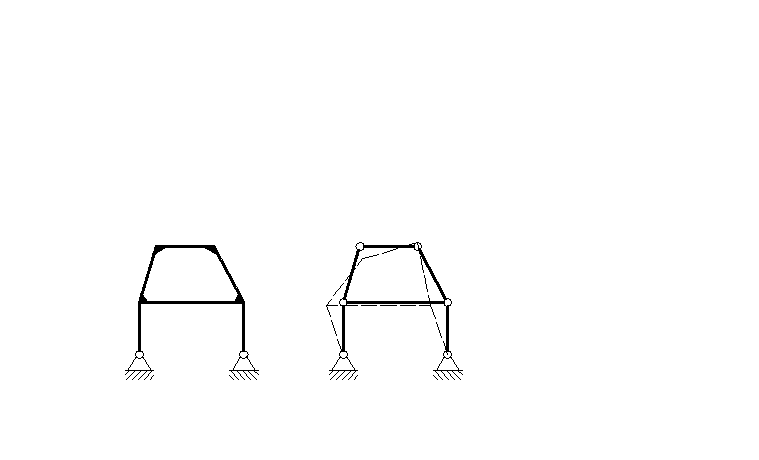
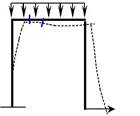
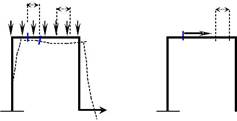
2 Рама – это стержневая система, геометрическая неизменяемость которой обеспечивается исключительно за счет жесткого соединения стержней в узлах.

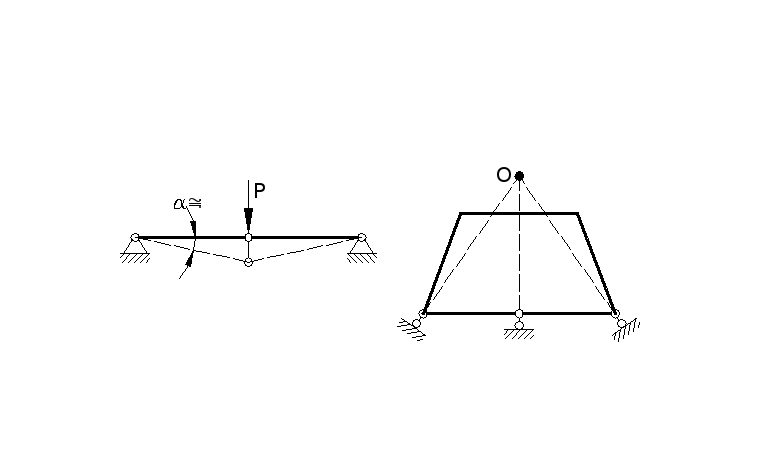
Признаком рамы является то, что при замене жестких узлов шарнирами, она превращается в механизм, то есть становится геометрически изменяемой, что не допустимо для расчетных схем (рис. 2).

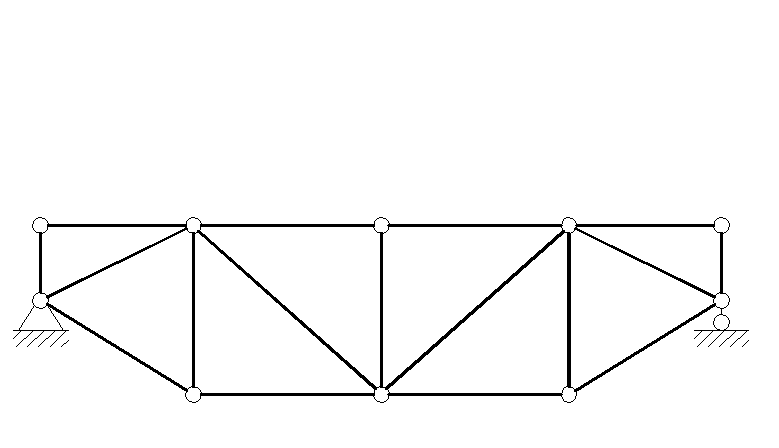
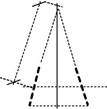
3 Ферма – это стержневая система, геометрическая неизменяемость которой обеспечена при шарнирном соединении концов стержней (рис. 3).

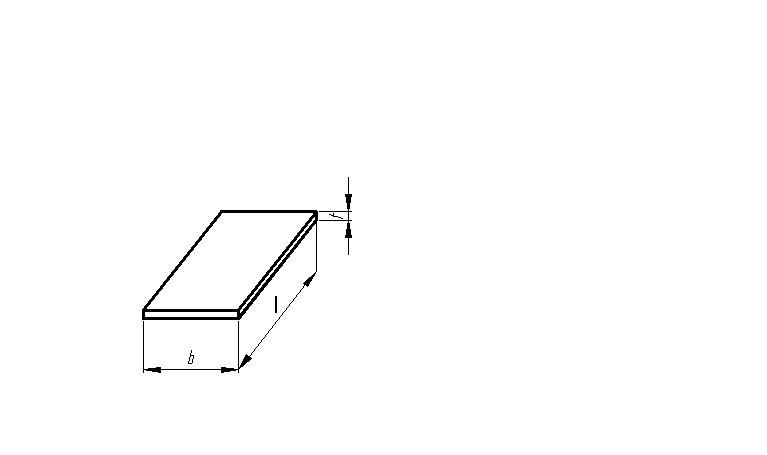
4 Пластина – это конструкция, образованная двумя параллельными плоскостями, расстояние между которыми значительно меньше двух других размер.

Рисунок 4 – Пример пластины

5 Оболочка – это конструкция, образованная двумя эквидистантными (на одном расстоянии) поверхностями, расстояние между которыми значительно меньше остальных размеров.

Рисунок 5 – Пример оболочки

6 Комбинированные расчетные схемы – получаются жестким или шарнирным соединением стержней, пластин и оболочек.

4 Общая характеристика и основные требования к расчетным схемам

Расчетная схема получается из схемы реального сооружения путем отбрасывания несущественных особенностей. В зависимости от того что принято за несущественные особенности, одна и та же конструкция (сооружение) может рассчитываться по разным расчетным схемам.

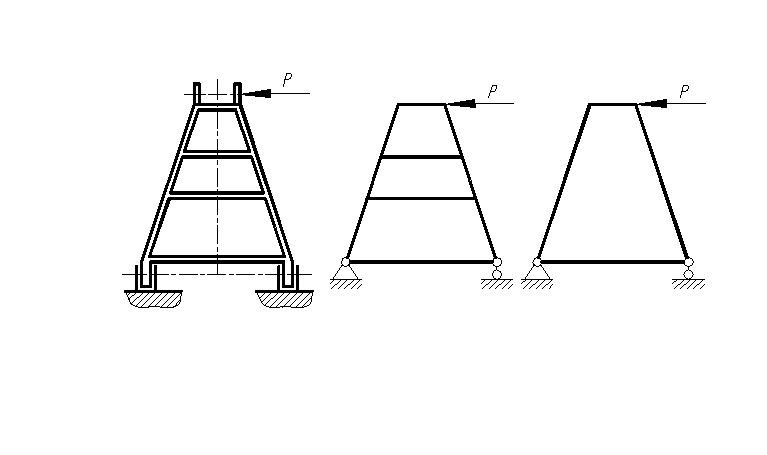
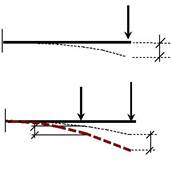
Пример выбора расчетной схемы для металлоконструкции стрелы железнодорожного крана.

Рисунок 6 – Примеры расчетных схем стрелы железнодорожного крана

К расчетным схемам предъявляются такие обязательные требования:

1 Расчетная схема должна быть геометрически неизменяема;

2 Все упрощения (отбрасывания несущественных особенностей) должны идти в запас надежности расчета, то есть расчетная схема должна быть слабее исходной схемы;

3 Расчетная схема должна быть неподвижно закреплена;

4 После отбрасывания опор и приложенных вместо них опорных реакций, схема должна находиться в равновесии:

5 Проверка расчетных схем на геометрическую неизменяемость

Эта задача заключается в определении степеней свободы системы. Системы могут состоять из стержней, пластин и оболочек соединенных между собой шарнирами. Эти стержни, платины и оболочки будем называть дисками. В таких системах различают простые и сложные шарниры.

Простой шарнир – соединяет между собой два диска

Рисунок 7 – Пример простого шарнира

Простой шарнир накладывает на систему две связи, то есть не допускает движение по x и y.

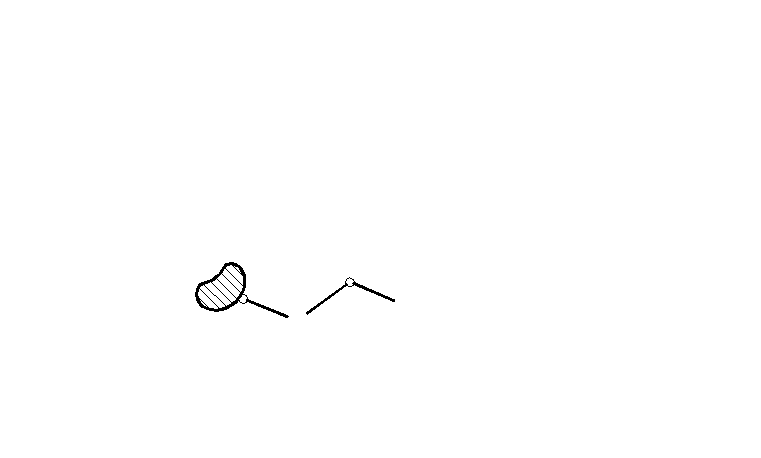
Сложный шарнир – соединяет в одной точке несколько дисков.

Рисунок 8 – Пример сложного шарнира

Если сложный шарнир соединяет n дисков, он будет эквивалентен n-1 простых шарниров. Поскольку каждый диск в свободном состоянии имеет три степени свободы, то общее число степеней свободы системы:

,

где Ш – число простых шарниров;

С – число связей с неподвижным основанием.

В результате подсчета может оказаться три случая:

1. W > 0 – система геометрически изменяема, что не допустимо.

3. W = 0 – эта система в большинстве случаев геометрически не изменяема и статически определима, но требуется проверка на мгновенную геометрическую изменяемость.

Рисунок 9 – Пример мгновенно изменяемых систем

Применение мгновенно изменяемых систем в качестве расчетных схем недопустимо.

Пример кинематического анализа

Проверить на геометрическую неизменяемость следующую систему.

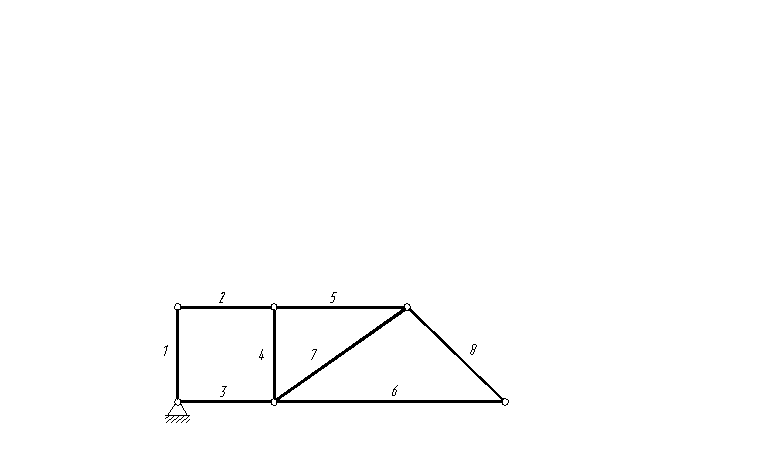
Рисунок 10 – Стержневая система

Стержневая система на рисунке 10 содержит 8 стержней (n=8), число простых шарниров Ш=10, числ связей с неподвижным основанием С=2.

.

Система имеет две степени подвижности, то есть не может использоваться в качестве расчетной схемы.

Список литературы: [2] с.3. 19; [6], с.5. 11; с. 7. 14; [7], с.5. 6; [18], с. 9. 23.

Источник

Частные случаи интеграла Мора

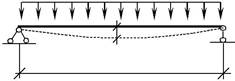
При расчете строительных конструкций по второй группе предель-ных состояний строительными нормами ограничивается максимальное пе-ремещение их точек. Это относится, прежде всего, к конструкциям, пере-крывающим большие пролеты. Величины максимально допустимых пере-мещений f выражаются в частях от пролета L (например, 1/300-1/500 от L) в зависимости от типа конструкции и условий ее работы (рис. 5.1).

Такая задача требует вычисления переме-щений точек системы. В этих случаях го-ворят о расчете конструкции на жест-кость.

Существует также целый ряд задач строительной механики, тре-бующие вычисления перемещений. Например, расчет статически неопре-делимых систем методом сил, динамический расчет и др.

Перемещения точек плоской стержневой системы будем обозначать буквой ∆ ( или δ) с двумя индексами ∆ _ij, где первый индекс i отмечает на-правление перемещения, а второй индекс j указывает на причину, вызы-вающую данное перемещение.

стержневой системы ∆ _K раскладывается на три со-

Укажем три основные причины возникновения перемещений:

– смещение опорных связей. Рассмотрим отдельно каждый случай.

Определение перемещений от силового воздействия

Действительное состояние –это состояние,на котором система де-формируется под действием силовой нагрузки (рис. 5.3).

Возможное (единичное) состояние–это состояние,когда система за-гружена единичным силовым фактором, приложенным по направлению ис-комого помещения.На рис. 5.4Показаны возможные состояния для опре-деления горизонтального, вертикального и углового перемещения точки k.

Рис. 5.4. Возможные состояния при определении:

а) горизонтального перемещения точки k;

б) вертикального перемещения точки k;

в) поворота сечения k.

Методы нахождения перемещений базируются на вычислении рабо-ты сил упругой системы. Необходимо различать понятия действительной и возможной работы сил на перемещениях.

F 2	F 1
∆ 22	∆ 12

Действительная работа –работа силы наперемещении, вызванном этой же силой. Такая работа равна половине произведе-нию силы на перемещение. Например, сила F ₁ совершает действительную работу наперемещении ∆ ₁₁.

Выражение такой работы будет T₁₁ = 1 ₂ F₁ ⋅ ∆₁₁ .

Например, для балки на рис. 5.5. Сила F ₂ совершает действительную работу T₂₂ = 1 ₂ F₂ ⋅ ∆₂₂ .

Возможная работа −это работа силы на перемещении,вызванномдругой силой. Она равна произведению силы на перемещение. Сила F ₁ со-вершает возможную работу на перемещении ∆ ₁₂ (это перемещение вызвано силой F ₂) по выражению T₁₂ = F₁ ⋅ ∆₁₂ . Здесь первый индекс связан с его

направлением перемещения,второй указывает номер силы,вызывающейэто перемещений.

Для деформируемой системы следует учесть работу как внешних сил (создающих деформации), так и внутренних сил, которые сопротивляются деформациям. Работу внешних сил будем обозначать T _ij.. Работу внутрен-них − W _ij.

Дальнейшие выводы сделаем на примере рамы , в которой требует-ся определить горизонтальное пе-ремещение точки k. Покажем действительное и возможное со-стояние рамы (рис. 5.6).

Рис. 5.6. Состояния рамы:

а) состояние1 (действительное состояние); б) состояние2 (возможное состояние)

Запишем выражение возможной работы силы F=1 возможного со-стояния (состояния 2) на перемещениях действительного состояния (со-стояния 1)

Далее определим выражение возможной работы внутренних сил состоя-ния 2 на перемещениях состояния 1.Для этого вырежем элементарный(бесконечно малый) участок рамы длиной ds. Деформации будем брать с действительного состояния,а внутренние усилия с возможного.Все уси-лия, относящиеся к возможному состоянию, обозначим подчеркиванием над символом. Будем считать, что перемещения возникают в результате деформаций изгиба и сжатия-растяжения. Тогда продольная сила будет совершать работу на удлинении (укорочении) стержня ∆ ds, а момент на угле поворота – d ϕ. Так как мы рассматриваем участок ds, это будет выра-жение элементарной работы dW _{2 1} = N· ∆ ds+M·d ϕ .

Далее выразим ∆ ds и d ϕ через ds. Так как осевая деформация стержня ε есть отношение приращения ∆ ds к первоначальной длине ds

(ε = ∆ _ds ds ), то ∆ ds = ε ·ds.

Источник

9.2 Вычисление интегралов Мора по правилу Верещагина

В реальных системах сечение по длине стержня не меняется, тогда величины жесткостей , , , можно вынести за знаки интегралов, тогда формула (1) примет вид:

В этих интегралах под интегралами стоят произведения двух функций. Одна функция, полученная из рассмотрения состояния заданного нагружения, а вторая – из единичного нагружения.

Поскольку единичное нагружение образуется единичной силой или единичным моментом, эпюры, от которых всегда линейны, то в подынтегральных выражениях вторая функция всегда линейна. Это обстоятельство позволяло предложить упрощенную методику вычисления интегралов Мора, путем перемножения эпюр получившее название правило Верещагина.

Согласно этому правилу интеграл Мора равен произведению площади эпюры от внешней нагрузки на ординату эпюры от единичной силы, взятую под центром тяжести первой эпюры. Площади и положения центров масс для типовых эпюр изгибающих моментов приведены на рисунке 32

Рисунок 32 – Перемножение эпюр по правилу Верещагина

В сопротивлении материалов и строительной механике существуют готовые таблицы результатов перемножения эпюр различных форм.

9.3 Частные случаи формулы Мора

9.3.1 Формула Мора для балок

В балках основным внутренним силовым фактором является изгибающий момент, а поперечные и продольные силы практически не оказывают влияния на прогиб, а потому ими можно пренебречь. Тогда в формуле Мора остается только первый интеграл. Кроме того, поскольку балка есть единичный стержень, то знак суммы будет отсутствовать, тогда формула Мора для балок примет вид:

9.3.2 Формула Мора для ферм

В стержнях ферм при правильном проектировании действуют только продольные силы, а изгибающие моменты и поперечные силы отсутствуют. Тогда в формуле Мора останется только второй интеграл. Кроме того, продольные силы всегда постоянны по длине стержней, а потому произведение N_p умноженное на N₁ можно вынести за знак интеграла, а интеграл:

.

Тогда формула Мора для ферм получит вид:

Расчет по этой формуле рекомендуется проводить в форме таблицы. Число строк в этой таблице всегда равно числу нагруженных стержней фермы.

Таблица 1 – Результаты расчета перемещений концов стержней фермы по формуле Мора

Для вычисления искомого перемещения необходимо сложить все цифры в графе 7.

9.4 Определение прогиба ферм как прогибов эквивалентных балок

Определение прогиба ферм по формуле Мора в виде таблицы отличается значительной трудоемкостью, а потому был предложен приближенный метод определения прогиба ферм как прогибов эквивалентных балок.

Эквивалентной называют такую балку, у которой прогиб в данном сечении такой же, как и у фермы при том же пролете и тех же нагрузках. Задача состоит в определении момента инерции эквивалентных балок, после чего для вычисления балок можно воспользоваться формулой Мора для балок.

Поскольку прогиб фермы определяется деформациями поясных стержней и стержней решетки, было предложено определять момент инерции эквивалентной балки как момент инерции поясов деленный на коэффициент, учитывающий влияние решетки:

.

Величина коэффициента зависит от конструкции решетки, и на практике можно принимать .

Рассмотрим поперечное сечение фермы, состоящее из одних поясов.

Рисунок 33 – Поперечное сечение фермы

x_в.п – x_в.п – собственная нейтральная ось сечения верхнего пояса;

x_н.п – x_н.п – собственная нейтральная ось сечения нижнего пояса;

x₀ – x₀ – нейтральная ось всего сечения;

a, b – расстояние нейтральной оси всего сечения до нейтральных осей, собственных, поясов.

Момент инерции всего сечения будет равен:

.

Практика показывает, что собственные моменты инерции крайне незначительны и ими можно пренебречь, тогда получим:

Рассматривая расстояние a и b как координаты всего сечения относительно осей x_в.п – x_в.п и x_н.п – x_н.п получим для них следующие выражения:

Подставляя формулы (2) в выражение (1) после преобразований получим окончательное выражение для моментов инерции поясов:

.

Источник