Бассейн наполняется двумя трубами за 10 ч за сколько часов бассейн наполнит первая труба

Вопрос по алгебре:

Бассейн наполняется двумя трубами за 10 ч. За сколько часов бассейн наполнит первая труба, если она это делает на 15 ч быстрее, чем первая

Ответы и объяснения 1

Если в лоб, то можно так. Пусть 2я труба наполнит за х ч. Тогда 1я за х+15 ч. При этом скорость наполнения для 1й 1/x (часть бассейна,наполняемая за 1 час ). А скорость 2й получается 1/(x+15).
Если они будут работать вместе, то скорость будет:
1/x+1/(1+15).
Соответственно при совместной работе они заполнят бассейн за
часов, что по условию равно 10 ч.

Отрицательный корень исключаем. Остается x=15.
Ответ: 2я труба наполняет бассейн за 15ч.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Источник

Бассейн наполняется двумя трубами за 10 ч. За сколько часов бассейн наполнит первая труба, если она это делает на 15 ч быстрее, чем первая

Отрицательный корень исключаем. Остается x=15.
Ответ: 2я труба наполняет бассейн за 15ч.

Косинус острого угла положителен.
Из основного тригонометрического тождества (тригонометрическая единица) следует, что

Sin²x — cos²x = cos4x ⇔ — (cos²x — sin²x) = cos4x ⇔ -cos2x =cos4x ⇔
0 =cos4x+cos2x ⇔2cos(4x -2x)/2 *cos(4x+2x) /2 =0 ⇔2cosx*cos3x =0 ⇒
[ cosx =0 ; cos3x =0 . ⇒ соs, 3x =π/2 +πn ,n∈Z. ⇔
[ x =π /2 +πk , x =π/6 +(π/3)*n ,k, n∈Z. ⇒ x = π/6 +(π/3)*n , n∈Z.
серия решения x = π/6 +(π/3)*n , n∈Z содержит и решения π/2 +πk , k∈Z при n =1 +3k .

ответ : π/6 +(π/3)*n , n∈Z.
* * * * * * *
cosx =0 ⇒ x = π/2 +πk , k∈Z
cos3x =0 ⇒ 3x = π/2 + πn ,n ∈Z ⇔ x = π/6 +πn /3 ,n ∈Z .
—
π/2 +πk = π/6 +πn /3 ⇔3 +6k =1 +2n ⇔ n =1 +3k
— или по другому:
cos3x =cosx(4cos²x -3)

Источник

Бассейн наполняется двумя трубами за 10 часов. За сколько часов наполнит бассейн первая труба, если она это делает на 15 ч быстрее, чем вторая?

Решение задач на работу

Вспомогательные задачи:

Задача№1

Условие

Весь бассейн заполнен – 1

Труба заполняет — за 3ч.

Труба заполняет – за 6ч

Какую часть каждая труба за 1ч?

(Надо найти производительность каждой трубы)

1) 1/3 (бассейна) – заполняет 1 труба.

2)1/6 (бассейна) – заполняет 2 труба.

Ответ. 1/3 и 1/6 часть бассейна.

Задача№2

Условие

Весь бассейн заполнен – 1

Труба за 1 час –1/3 часть

Труба за 1 час – 1/6часть

Какая часть обоими трубами (совместно) за 1 час ?

За сколько часов заполнится весь бассейн? (при совместной работе)

1)1/3 + 1/6 = 3/6 = ½ (бассейна) заполняют обе трубы за 1ч.

2) 1: ½ = 2 (часа) – заполнится весь бассейн при совместной работе труб.

Ответ. ½ часть. За 2 часа.

Задача№3

Запиши условие

Весь путь — 1.

Путешественник – 10 дней.

Путешественник — 15 дней.

Через сколько дней они встретятся;

1) 1/10 (пути) – проходит 1 путешественник за 1 день.

2) 1/15 (пути) – проходит 2 путешественник за 1 день.

3) 1/10 + 1/15 = 5/30 = 1/6 (пути) – проходят путешественники вместе за 1 день.

4) 1:1/6 = 6 (дней) – пройдут весь путь (встретятся)

Ответ. Через 6 дней.

ПРИНИМАЙ ВСЮ РАБОТУ ЗА ЕДИНИЦУ (1).

НАЙДИ ЧАСТЬ РАБОТЫ В ЕДИНИЦУ v = 1/t
ВРЕМЕНИ (производительность)

Читайте также: Проект бассейн для частного дома
ЕСЛИ НУЖНО, НАЙДИ ВРЕМЯ t = 1/v
СОВМЕСТНОЙ РАБОТЫ

Задача№1

Для вывоза песка из карьера в автопарке было заказано несколько одинаковых грузовых автомобилей. Руководство автопарка решило, что на каждую машину можно погрузить на одну тонну груза больше, чем рассчитывали, и поэтому прислало на 4 машины меньше. В итоге все 80 тонн песка были вывезены. Сколько машин было заказано в автопарке?

Задача№2

Ученик решил прочитать книгу, содержащую 480 страниц, за несколько дней. Но каждый день он читал на 20 страниц больше, чем предполагал, и поэтому прочитал книгу на 4 дня раньше. За сколько дней была прочитана книга?

Пусть х страниц предполагал читать ученик в день, тогда 480/х дней предполагал ученик читать книгу.

Фактически читал ученик в день — (х+20) страниц, тогда 480/(х+20) дней фактически читал ученик книгу.

Т.к. он прочитал книгу на 4 дня раньше, составляем уравнение:

120х+2400-120х=х 2 +20х

х₁=-60 не удовлетворяет условию задачи

х₂=40, х+20=60, 480:60=8(дней) читал ученик книгу. Ответ: 8 дней.

Задача№3

Бассейн наполняется двумя трубами за 10 часов. За сколько часов наполнит бассейн первая труба, если она это делает на 15 ч быстрее, чем вторая?

Для начала вспомним формулу для вычисления объёма проделанной работы: А=vt.

Обратите внимание на то, что здесь есть полное соответствие задачам на движение: путь – объём работы, скорость – производительность, время – время.

Сначала перепишем условие на математическом языке.

Работа по наполнению бассейна объёмом A выполнена двумя трубами одновременно с общей скоростью за время t=10 ч.

Первая труба наполняет бассейн (объём работы ) со скоростью за время .

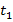
Вторая труба наполняет бассейн (объём работы ) со скоростью за время .

Обратите внимание на то, что в подобных задачах на совместную работу производительности складывать можно, а времена – нет.

А = 10/ ( ), отсюда следует, =А/10

А= , отсюда следует, =А/

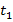
А= . отсюда следует, =А/

Так как трубы заполняют один и тот же бассейн, то есть выполняют одинаковую работу, то можно принять работу за 1.

Источник

Бассейн наполняется двумя трубами за 10 ч. За сколько часов бассейн наполнит первая труба, если она это делает на 15 ч быстрее, чем первая

Ответы:

Ответы на похожие вопросы:

О, Господи! ты онлайн переводчиком с какого-то языка переводил?Я так понял, что площадь дорожки шириной x= 0,5м,вокруг басейна 15м^2. это значит, что длина дорожки вокруг басейна P=S/x = 15/0,5=30mто есть периметр басейна P= сумме длин всех сторон басейна , скажем Х+Х+У+У=30 иХ+6=У — одна сторона на 6м длиннеетогда 2*(Х+6)+2*Х=30 тогда 4Х=28, Х=7 У=13

F(x) браток делается с дальность 7.8.6

Читайте также: Бассейны с подогревом под открытым небом
две трубы —- 6 час ,1-я труба —— 15 час,2-я труба —— ? часРешение.Х час —- время заполнения бассейна только второй трубой,1/Х —— часть бассейна, заполняемая второй трубой за 1 час,1/15 —- часть бассейна, заполняемая первой трубой за 1 час,1/6 —— часть бассейна, заполняемая за 1 час двумя трубами,1/15 + 1/Х = 1/6 —— вклад каждой из труб в заполнение бассейна в час,1/Х = 1/6 — 1/15 —— выражение для части бассейна, заполняемой за час второй трубой через разность частей в час совместной работы и первой трубы,1/Х = 5/30 — 2/30 = (5-2)/30 = 3/30 = 1/10,1/Х = 1/10, Х =10,Ответ: вторая труба заполнит бассейн за 10 часов.Проверка: (1/10)+(1/15)=(1/6), 1/6 = 1/6

Прости я не знаю тебе сколько лет

15м²:0,5=30м-длина дорожки или Р бассейнах м-ширина бас.х+6 м -длина бас.(х+х+6)х2=302х+2х+12=302х+2х=30-124х=18х=18:4х=4,5м-ширина бас.4,5+6=10,5м-длина бас

Будем решать в минутах:

1 час 45 минут=105 минут

1 час 15 минут=75 минут

2 часа 55 минут=175 минут

a,b,c,d — производительности 1,2,3,4 трубы

Будем решать систему уравнений метод сложения.То есть, складываем все левые части и приравниваем их к сумме вторых частей уравнений:

Значит, если включить все 4 трубы, то бассейн заполнится за 70 минут или 1 час и 10 минут.

Дано:Vнаполнения=1/t1Vопорожнияя=1/t2t1=4чt2=8чРешение:Vнаполнениявместесопорожнением=1/t1-1/t2=1/4-1/8=1/8Ответ 8 часов

1/6 наливается за 1ч1/10-выливается за 1ч1/6-1/10=(5-3)/30=2/30=1/15-наполняется за 1ч1:1/15=15 часов бассейн заполнится

Попробуй1)12-7=5а дальше хз?

Первая в час заполняет бассейн на 1/12. а вторая за 1/24. вместе за час они заполнят 1/12+1/24=3/24=1/8следовательно за 8 часов заполнится бассейн

Пусть ребро первого куба х. Тогда ребро второго 2хОбъем первого куба х³, объём второго бассейна (2х)³=8х³Значит на второй бассейн потребуется в 8 раз больше времени,т.е.8*40=320 минут = 5 часов 20 минутОтвет: не успеет

21р20к-100%х р -9%х=(9*21,2)/100=1,908=1,91 скидка21,2-1,91=19,29 стоит 1 батарейка со скидкой240:19,29=12,44ответ 12 батареек

Р=2(а+в) — формула периметрав=Р/2-аа=13 Р=38в=38/2-13=19-13=6в=6

Источник

Бассейн наполняется двумя трубами за 10 ч за сколько часов бассейн наполнит первая труба

Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

Пусть объем бассейна равен 1. Обозначим и — скорости наполнения бассейна первой и второй трубой, соответственно. Две трубы наполняют бассейн за 3 часа 36 минут:

По условию задачи одна первая труба наполняет бассейн за 6 часов, то есть Таким образом,

Тем самым, вторая труба за час наполняет 1/9 бассейна, значит, вторая труба наполняет этот бассейн за 9 часов.

Приведем другое решение.

Первая труба за час наполняет 1/6 бассейна, значит, за 3 ч 36 мин = 3,6 часа она заполнит 0,6 бассейна. Следовательно, вторая труба за 3,6 часа заполнит 0,4 бассейна. Поэтому весь бассейн она заполнит за время 3,6:0,4 = 9 часов.

Источник