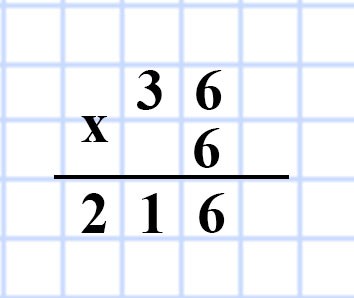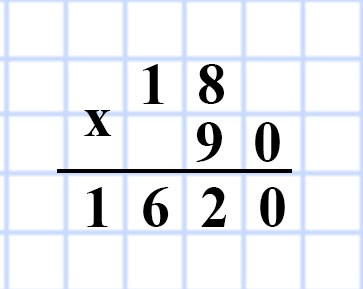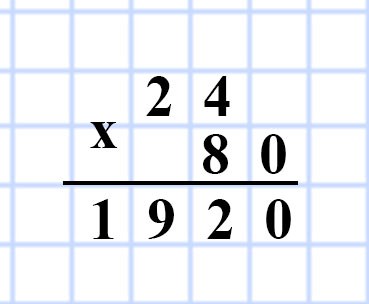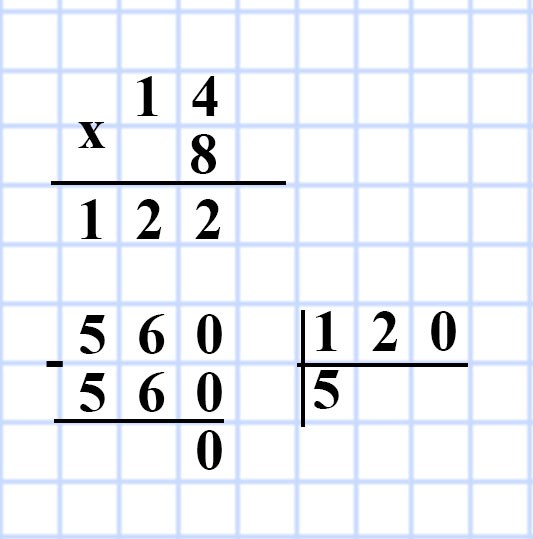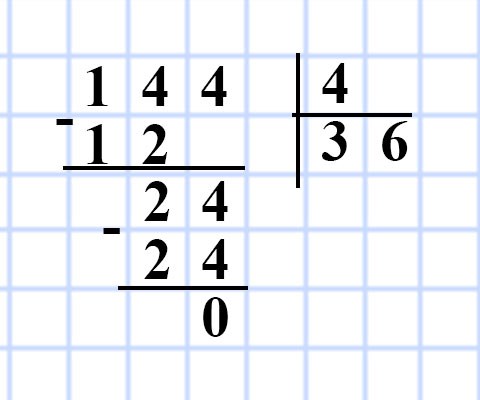Мерзляк 5 класс — § 23. Объём прямоугольного параллелепипеда
Вопросы к параграфу
1. Какими свойствами обладает объём фигуры?
- Равные фигуры имеют равные объёмы.
- Объём фигуры равен сумме объёмов фигур, из которых она состоит.
2. Какой куб называют единичным?
Единичным называют куб, ребро которого равно единичному отрезку.
3. Приведите примеры единиц измерения объёма.
- 1 мм³ — один кубический миллиметр
- 1 см³ — один кубический сантиметр
- 1 дц³ — один кубический дециметр
- 1 м³ — один кубический метр
- 1 л — один литр (при измерении жидкостей, 1 л = 1 дм³)
4. Что означает измерить объём фигуры?
Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.
5. Чему равен объём прямоугольного параллелепипеда с измерениями а, b, с?
V = abc
6. По какой формуле вычисляют объём куба?
V= a³
7. Как вычислить объём прямоугольного параллелепипеда, зная его площадь основания и высоту?
V = Sh
Решаем устно
1. Заполните пропуски в цепочке вычислений:
2. Сколько необходимо использовать кубиков с ребром 1 см, чтобы сложить кубик с ребром 2 см?
Чтобы сложить кубик с ребром 2 см, надо использовать 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?
3 • 4 + 5 • 4 + 6 • 4 = 12 + 20 + 24 = 56 (см) — проволоки.
4. Расставьте вместо звёздочек знаки «+» и «—» так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.
20 + 30 — 10 + 80 — 70 = (20 + 30) + (80 — 10 — 70) = 50 + 0 = 50
Упражнения
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
- 1 дм = 10 см
- 1 дм² = 10 см • 10 см = 100 см²
- 1 дм³ = 10 см • 10 см • 10 см = 1 000 см³
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
- 1 м = 100 см
- 1 м² = 100 см • 100 см = 10 000 см²
- 1 м³ = 100 см • 100 см • 100 см = 1 000 000 см³
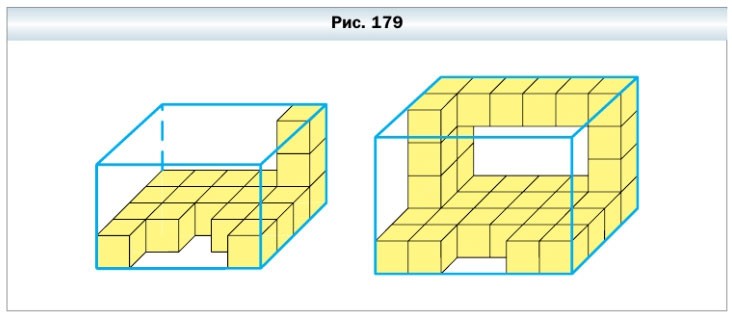
618. Фигуры, изображённые на рисунке 179, сложены из кубиков, рёбра которых равны 1 см. Найдите объём каждой фигуры.
Для того, чтобы найти объём фигуры, надо посчитать количество единичных кубов, из которых она состоит.
1 фигура (на рисунке слева):
V = 5 • 2 + 3 + 3 + 2 = 10 + 8 = 18 см³
2 фигура (на рисунке справа):
V = 6 • 3 + 2 +2 + 3 • 2 + 5 + 2 = 18 + 4 + 6 + 7 = 18 + 17 = 35 см³
Ответ: 18 см³ и 35 см³.
619. Вычислите объём прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
Дано:
a = 12 м
b = 15 м
c = 6 м
V = ? м³
Решение:
V = abc = 12 • 15 • 6 = 12 • 90 = 1 080 м³
620. Чему равен объём куба, ребро которого равно 6 см?
Дано:
Решение:
V= a³ = 6³ = 36 • 6 = 216 см³
621. Чему равен объём прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
Дано:
a = 10 дм
b = 8 дм
c = 4 дм
V = ? дм³
Решение:
V = abc = 10 • 8 • 4 = 10 • 32 = 320 дм³
622. Выразите:
1) в кубических миллиметрах:
38 см³ = 38 000 мм³
12 см³ 243 мм³ = 12 000 мм³ + 243 мм³ = 12 243 мм³
42 см³ 68 мм³ = 42 000 мм³ + 68 мм³ = 42 068 мм³
54 см³ 4 мм³; = 54 000 мм³ + 4 мм³ = 54 004 мм³
1 дм³ 20 мм³ = 1 000 000 мм³ + 20 мм³ = 1 000 020 мм³
18 дм³ 172 см³ = 18 000 000 мм³ + 172 000 мм³ = 18 172 000 мм³
35 дм³ 67 см³ 96 мм³ = 35 000 000 мм³ + 67 000 мм³ + 96 мм³ = 35 067 096 мм³
2) в кубических дециметрах:
264 м³ = 264 000 дм³
10 м³ 857 дм³ = 10 000 дм³ + 857 дм³ = 10 857 дм³
28 м³ 2 дм³ = 28 000 дм³ + 2 дм³ = 28 002 дм³
44 000 см³ = 44 дм³
5 430 000 см³ = 5 430 дм³
623. Выразите в кубических сантиметрах:
62 дм³ = 62 000 см³
378 000 мм³ = 378 см³
520 000 мм³ = 520 см³
78 дм³ 325 см³ = 78 000 см³ + 325 см³ = 78 325 см³
56 дм³ 14 см³ = 56 000 см³ + 14 см³ = 56 014 см³
8 м³ 4 дм³ 6 см³ = 8 000 000 см³ + 4 000 см³ + 6 см³ = 8 004 006 см³
624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота — в 3 раза меньше длины. Найдите объём данного параллелепипеда.
Дано:
a = ? см, на 3 дм больше, чем ребро b
b = 15 дм
c = ? см, в 3 раза меньше, чем ребро a
V = ? см³
Решение:
1) 15 + 3 = 18 (дм) — длина прямоугольного параллелепипеда.
2) 18 : 3 = 6 (дм) — высота прямоугольного параллелепипеда.
3) 18 • 15 • 6 = 18 • 90 = 1 620 (дм³) — объем V прямоугольного параллелепипеда.
Ответ: V= 1 620 дм³.
625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объём данного параллелепипеда.
Дано:
a = ? см, на 4 см больше, чем ребро с
b = ? см, в 5 раз меньше, чем ребро c
c = 20 см
V = ? см³
Решение:
1) 20 + 4 = 24 (см) — длина прямоугольного параллелепипеда.
2) 20 : 5 = 4 (см) — ширина прямоугольного параллелепипеда.
3) 24 • 5 • 20 = 24 • 80 = 1 920 (дм³) — объем V прямоугольного параллелепипеда.
Ответ: V= 1 920 дм³.
626. Объём прямоугольного параллелепипеда равен 560 см³, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.
Дано:
a = 14 см
b = 8 см
V = 560 см³
h = ? см
Решение:
V = Sh, значит h = V : S
1) 14 • 8 = 122 (см²) — площадь основания S прямоугольного параллелепипеда.
2) 560 : 120 = 5 (см) — высота h прямоугольного параллелепипеда.
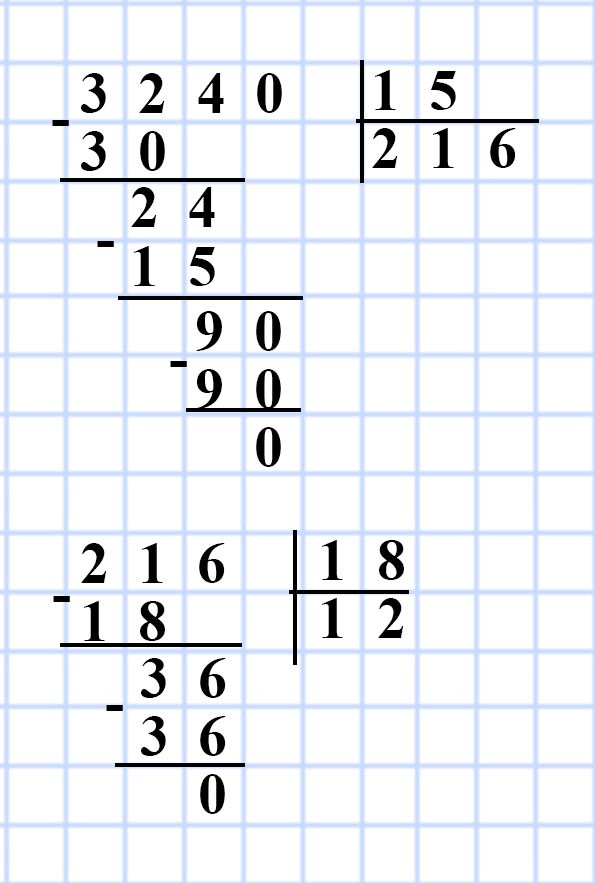
627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объём — 3 240 см³. Найдите ширину данного параллелепипеда.
Дано:
a = 18 см
h = 15 см
V = 3 240 см³
b = ? см
Решение:
V = Sh, значит S = V : h
1) 3 240 : 15 = 216 (см²) — площадь основания S прямоугольного параллелепипеда.
S = a • b, значит b = S : a
2) 216 : 18 = 12 (см) — ширина b прямоугольного параллелепипеда.
628. Объём комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м³, а высота — 4 м. Найдите площадь пола комнаты.
Дано:
h = 4 м
V = 144 м³
S = ? м²
Решение:
V = Sh, значит S = V : h
1) 144 : 4 = 36 (м²) — площадь пола комнаты.
629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объём равен 960 м³, а площадь пола равна 192 м². Найдите высоту спортивного зала.
Дано:
S = 192 м²
V = 960 м³
h= ? м
Решение:
V = Sh, значит h = V : S
1) 960 : 192 = 5 (м) — высота спортивного зала.
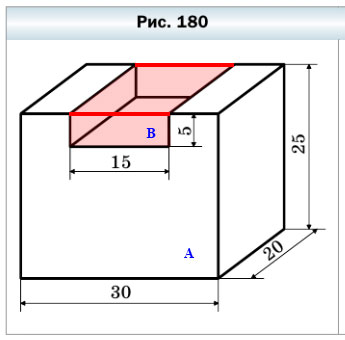
630. Найдите объём фигуры, изображённой на рисунке 180 (размеры даны в сантиметрах).
Выполним дополнительное построение: проведём линии, соединяющие выступающие части исходной фигуры. Теперь можно сказать, что V = VА— VВ, где:
- V — объем искомой фигуры.
- VА — объем большого прямоугольного параллелепипеда, измерения которого равны 30 см, 20 см и 25 см.
- VВ — объем малого прямоугольного параллелепипеда (красный), который вырезали из большого параллелепипеда для получения искомой фигуры. Его измерения: 15 см, 5 см и 20 см.
VА = 30 • 20 • 25 = 600 • 25 = 15 000 (cм³)
VА = 15 • 5 • 20 = 15 • 100 = 1 500 (cм³)
V = VА— VВ = 15 000 — 1 500 = 13 500 (cм³)
Ответ: V= 13 500 cм³
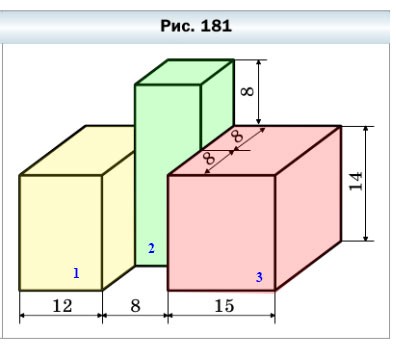
631. Найдите объём фигуры, изображённой на рисунке 181 (размеры даны в сантиметрах).
Фигуру, изображенную на рисунке 181, можно разделить на три прямоугольных параллелепипеда:
Рассмотрим прямоугольный параллелепипед № 3 (красный):
- длина равна 15 см
- ширина равна 8 + 8 = 16 см
- высота равна 14 см
V3 = 15 • 16 • 14 = 240 • 14 = 3 360 (cм³)
Рассмотрим прямоугольный параллелепипед № 2 (зелёный):
- длина равна 8 см
- ширина равна 8 см
- высота равна 14 + 8 = 22 см
V2 = 8 • 8 • 22 = 64 • 22 = 1 408 (cм³)
Рассмотрим прямоугольный параллелепипед № 1 (жёлтый):
- длина равна 12 см
- ширина равна 8 + 8 = 16 см
- высота равна 14 см
V1 = 12 • 16 • 14 = 192 • 14 = 2 688 (cм³)
Объем фигуры равен сумме объемов фигур, из которых она состоит.
V = V1 + V2 + V3= 2 688 + 1 408 + 3 360 = 7 456 (cм³)
Ответ: V = 7 456 cм³.
632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см³ цинка составляет 7 г.
Дано:
a = 4 cм²
Масса 1 cм³ = 7 г
Масса куба = ? г
Решение:
V = 4 • 4 • 4 = 16 • 4 = 64 (см³)
Масса 1 см³ куба равна 7 г, значит масса 64 см³ равна:
633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм³ земли?
150 м = 15 000 см
1) 15 000 • 80 • 60 = 1 200 000 • 60 = 72 000 000 (см³) — объем выкопанной машиной траншеи.
72 000 000 см³ = 72 м³
2) 72 : 8 = 9 (м³) — выкапывает машина за 1 час.
72 м³ = 72 000 дм³
3) 72 000 : 240 = 300 (человек) — коротышек могут заменить 1 машину.
Ответ: 9 м³, 300 коротышек.
634. Куб и прямоугольный параллелепипед имеют равные объёмы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.
1) 12 • 2 = 6 (см) — сторона b прямоугольного параллелепипеда.
2) 12 • 4 = 3 (см) — сторона с прямоугольного параллелепипеда.
3) V = a • b • c = 12 • 6 • 3 = 72 • 3 = 216 (см³) — объём прямоугольного параллелепипеда.
V (прямоугольного параллелепипеда) = V (куба) = a³ = 216 (см³)
Значит сторона куба равна такому числу, которое при возведении в третью степень равно 216. Методом подбора можем определить что это число 6, то есть сторона квадрата а = 6 см.
У куба 6 одинаковых граней, площадь каждой из которых равна а².
4) а² = 6 • 6 = 36 (см²) — площадь поверхности одной грани куба.
5) 36 • 6 = 216 (см²) — площадь поверхности куба.
Ответ: Площадь поверхности куба равна 216 см².
635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объём первого куба больше объёма второго?
Пусть длина ребра второго куба равна х единиц, тогда длина ребра первого куба будет равна 4х единиц.
S2 = 6a² = 6x² (ед²) — площадь поверхности второго куба.
S1 = 6a² = 6(4x)² = 6 • (4 • 4 • x • x) = 6 • 16 x² = 96 x² (ед²) — площадь поверхности первого куба.
S2 : S1 =96 x² : 6x² = 96 : 6 = 16 (раз) — площадь поверхности первого куба больше площади поверхности второго куба.
V2 = a³ = х³ (ед³) — объём второго куба.
V1 = a³ = (4х)³ = 4 • 4 • 4 • x • x • x = 16 • 4 • х³ = 64 х³ (ед³) — объём второго куба.
V1 : V2= 64 х³ : х³ = 64 (раза) — объём первого куба больше объёма второго куба.
Ответ: Площадь поверхности больше в 16 раз, объём больше в 64 раза.
636. Как изменится объём прямоугольного параллелепипеда, если:
1) длину увеличить в 4 раза, ширину — в 2 раза, высоту — в 5 раз
V1 = (4 • a) • (2 • b) • (5 • c) = (4 • 2 • 5) abc = 40 abc
V1 : V = 40 abc : abc = 40 (раз)
Ответ: объём увеличится в 40 раз.
2) ширину уменьшить в 4 раза, высоту — в 2 раза, а длину увеличить в 16 раз
V1 = (16 • a) • (b : 4) • (c : 2) = (16 : 4 : 2) abc = (4 : 2) abc = 2 abc
V1 : V = 2 abc : abc = 2 (раза)
Ответ: объём увеличится в 2 раза.
637. Как изменится объём прямоугольного параллелепипеда, если:
1) каждое измерение увеличить в 2 раза
V1 = (2 • a) • (2 • b) • (2• c) = (2 • 2 • 2) abc = 8 abc
V1 : V = 8 abc : abc = 8 (раз)
Ответ: объём увеличится в 8 раз.
2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз
V1 = (a : 3) • (b • 15) • (c : 5) = (15 : 3 : 5) abc = (5 : 5) abc = abc
V1 : V = abc : abc = 1 (раз)
Ответ: объём не изменится.
638. В бассейн, площадь дна которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?
S = 1 га = 10 000 м² = 1 000 000 дм²
V = 1 000 000 л = 1 000 000 дм³
V = S • h, значит h = V : S
h = V : S = 1 000 000 дм³ : 1 000 000 дм² = 1 дм = 10 см — высота налитой в басейн воды.
Это значит, что плавать в этом бассейне невозможно.
Ответ: Нет, соревнования по плаванию провести нельзя.
639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объём оставшейся части.
1) V (куба) = a³ = 3³ = 9 • 3 = 27 (см³) — объём куба с ребром 3 см.
2) V (одного отверстия) = abc = 1 • 1 • 3 = 3 (см³) — объем одного сквозного отверстия со стороной 1 см.
Так как все три отверстия пересекаются в центре куба, то объём вырезанной части:
3) V (вырезанной части) = 3 см³ • 3 ( размер трёх сквозных отверстий) — 1 см³ (размер пересечения второго отверстия в первым и третьим) — 1 см³ размер пересечения третьего отверстия с первым и вторым) = 9 — 1 — 1 = 7 (см³) — объём вырезанной части.
4) V (оставшейся части) = V (куба) — V (вырезанной части) = 27 — 7 = 20 (см³) — объём оставшейся части.
640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?
1) 12 • 6 • 4 = 72 • 4 = 288 (см³) — объём нового куска мыла.
2) (12 : 2) • (6 : 2) • (4 : 2) = 6 • 3 • 2 = 18 • 2 = 36 (см³) — объём мыла через 14 дней использования.
3) 288 — 36 = 252 ( см³) — мыла было использовано за 14 дней.
4) 252 : 14 = 18 (см³) — мыла используется за 1 день.
5) 36 : 18 = 2 (дня) — хватит оставшегося мыла.
Упражнения для повторения
641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?
1) 350 = 2 • 160 + 30 (см)
Значит, для того, чтобы покрыть линолеумом в один ряд пол по ширине коридора необходимо использовать 2 рулона материала и ещё полосу шириной в 30 см.
2) 30 = 12 • 2 + 6 (м)
Значит, для того, чтобы покрыть линолеумом в один ряд пол по длине коридора необходимо использовать 2 целых рулона и ещё одну половину рулона (6 = 12 : 2).
- 1 ряд по длине — 2 рулона + полоса 12 м х 30 см
- 2 ряд по длине — 2 рулона + полоса 12 м х 30 см
- 3 ряд по длине — (половина рулона + половина рулона) + полоса 6 м х 30 см.
Половина рулона + половина рулона = 1 целый рулон.
Полосы 12 м х 30 см, 12 м х 30 см и 6 м х 30 см можно выкроить из 1 целого рулона.
Значит нам потребуется:
3) 2 + 2 + 1 + 1 = 6 (шт) — рулонов линолеума потребуется для замены линолеума в школьном коридоре.
Ответ: 6 рулонов.
642. Из двух населённых пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?
1) 12 • 2 = 24 (км) — проехал первый велосипедист до места встречи.
2) 54 — 24 = 30 (км) — проехал второй велосипедист до места встречи.
3) 30 : 2 = 15 (км/ч) — скорость второго велосипедиста.
643. Найдите значение выражения:
1) 7a + 7b, если a + b = 14
7a + 7b = 7 (a + b) = 7 • 14 = 98
2) m • 17 + n • 17, если m + n = 1 000
m • 17 + n • 17 = 17 (m + n) = 17 • 1 000 = 17 000
3) k • 9 + 9l, если k + l = 12
k • 9 + 9l = 9 (k + l) = 9 • 12 = 108
4) 4c — 4d, если с — d = 125
4c — 4d = 4 (c — d) = 4 • 125 = 500
5) x • 23 — 23y, если x — у = 4
x • 23 — 23y = 23 (x — y) = 23 • 4 = 92
6) 56p — r • 56, если р — r = 11
56p — r • 56 = 56 (p — r) = 56 • 11 = 616
Задача от мудрой совы
644. В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
Если в записи первого трёхзначного числа используются только цифры 2 и 3, то таким трёхзначным числом могут быть числа:
- 222, 223, 232, 322, 233, 323, 332, 333.
Если в записи второго трёхзначного числа используются только цифры 3 и 4, то таким трёхзначным числом могут быть числа:
- 333, 334, 343, 433, 344, 434, 443, 444.
Расположим их в виде таблицы:
- в первом столбце напишем все возможные варианты первого числа;
- в верхней строке — все возможные варианты второго числа;
- на пересечении — произведение соответствующего варианта первого и второго числа (можно их посчитать при помощи калькулятора).
| 334 | 343 | 433 | 344 | 434 | 443 | 73926 | 74148 | 76146 | 96126 | 76368 | 96348 | 98346 | 98568 | ||
| 74259 | 74482 | 76489 | 96559 | 76712 | 96782 | 98789 | 99012 | ||||||||
| 232 | 77256 | 77488 | 79576 | 100456 | 79808 | 100688 | 102776 | 107226 | 107548 | 110446 | 139426 | 110768 | 139748 | 142646 | 142968 |
| 233 | 77589 | 77822 | 79919 | 100889 | 80152 | 101122 | 103219 | 107559 | 107882 | 110789 | 139859 | 111112 | 140182 | 143089 | 143412 |
| 332 | 110556 | 110888 | 113876 | 143756 | 114208 | 144088 | 147076 | ||||||||
| 333 | 110889 | 111222 | 114219 | 144189 | 114552 | 144522 | 147519 |